
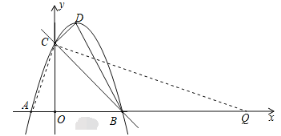
【題目】如圖,以![]() 為頂點的拋物線
為頂點的拋物線![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() ,交
,交![]() 軸于點
軸于點![]() .
.
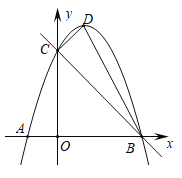
(1)求拋物線的解析式;
(2)在直線![]() 上有一點
上有一點![]() ,使
,使![]() 的值最小,求點
的值最小,求點![]() 的坐標;
的坐標;
(3)在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)點
;(2)點![]() 的坐標為
的坐標為![]() ;(3)存在,當
;(3)存在,當![]() 的坐標為
的坐標為![]() 或
或![]() 時,以
時,以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.
相似.
【解析】
(1)將點B和點C的坐標代入二次函數解析式中即可求出結論;
(2)先求出點A的坐標,利用待定系數法求出BC的解析式,作點O關于BC的對稱點O′,連接AO′交BC于點P,連接OP,O′B,根據兩點之間線段最短,此時![]() 最小,求出點O′的坐標,利用待定系數法求出AO′的解析式,聯立方程即可求出結論;
最小,求出點O′的坐標,利用待定系數法求出AO′的解析式,聯立方程即可求出結論;
(3)求出頂點D的坐標,利用平面直角坐標系中任意兩點之間的距離公式求出CD、BC、CD和AC,根據勾股定理的逆定理證出△BCD是直角三角形,然后根據相似三角形的對應情況分類討論,根據相似三角形的性質列出比例式即可求出結論.
解:(1)將點B和點C的坐標代入![]() 中,得
中,得
![]()
解得: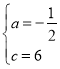
∴拋物線的解析式為![]() ;
;
(2)把y=0代入![]() 中,得
中,得
![]()
解得:x1=-2,x2=6,
∴點A的坐標為(-2,0)
設直線BC的解析式為y=kx+b
將點B和點C的坐標代入,得
![]()
解得:![]()
∴直線BC的解析式為![]()
作點O關于BC的對稱點O′,連接AO′交BC于點P,連接OP,O′B
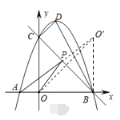
根據對稱可得PO=PO′,OB=O′B
此時![]() =
=![]() =
=![]()
根據兩點之間線段最短,此時![]() 最小
最小
∵OB=OC=6,∠BOC=90°
∴∠OBC=45°
∴∠OBO′=90°
∵OB= O′B =6
∴點O′的坐標為(6,6)
設直線AO′的解析式為y=mx+n
將點A和點O′的坐標代入,得
![]()
解得: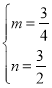
∴直線AO′的解析式為![]()
聯立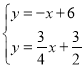
解得: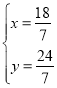
∴點P的坐標為![]()
(3)∵![]() =
=![]()
∴點D的坐標為(2,8)
∴![]()
![]()
∴CD2+BC2=80=BD2
∴△BCD為直角三角形,且∠BCD=90°
點Q在點A左側時,△QAC為鈍角三角形,
∴△QAC不可能與△BCD相似
∴點Q必在點A右側,設點Q的坐標為(q,0),則AQ=q-(-2)=q+2
∵tan∠CAO=![]() ,tan∠BDC=
,tan∠BDC=![]()
∴∠CAO=∠BDC
當△CQA∽△BCD時,
∴![]()
即![]()
解得:q=0
∴點Q的坐標為(0,0);
當△QCA∽△BCD時,
∴![]()
即![]()
解得:q=18
∴點Q的坐標為(18,0);
綜上:點Q的坐標為![]() 或
或![]() .
.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案 寒假創新型自主學習第三學期寒假銜接系列答案
寒假創新型自主學習第三學期寒假銜接系列答案科目:初中數學 來源: 題型:
【題目】在一次數學測驗中,八年級(1)班的成績如下表:
分數 | 65 | 70 | 75 | 80 | 85 | 90 | 95 | 100 |
人數 | 2 | 3 | 10 | 6 | 4 | 7 | 6 | 2 |
(1)本次數學測驗成績的平均數,中位數,眾數各是多少?
(2)若老師把人數中的數據“10”看成了“9”,數據“7”看成了“8”,則平均數,中位數,眾數中不受影響的是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
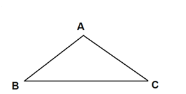
【題目】如圖,在△ABC中,AB=AC.
(1)若以點A為圓心的圓與邊BC相切于點D,請在下圖中作出點D;(要求:尺規作圖,不寫作法,保留作圖痕跡)
(2)在(1)的條件下,若該圓與邊AC相交于點E,連接DE,當∠BAC=100°時,求∠AED的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知Rt△EBC中,∠B=90°,A為BE邊上一點,以邊AC上的點O為圓心、OA為半徑的圓O與EC相切,D為切點,AD∥BC.
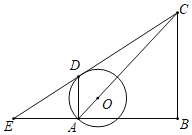
(1)求證:∠E=∠ACB.
(2)若AD=1,![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形![]() 中,
中,![]() ,點
,點![]() ,
,![]() 分別在
分別在![]() ,
,![]() 上,將
上,將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在
落在![]() 上的點
上的點![]() 處,又將
處,又將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在直線
落在直線![]() 與
與![]() 的交點
的交點![]() 處.
處.
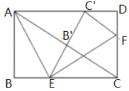
(1)求證:點![]() 在
在![]() 的角平分線上;
的角平分線上;
(2)求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
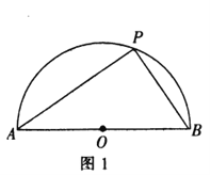
【題目】[問題發現]如圖1,半圓![]() 的直徑
的直徑![]() 是半圓
是半圓![]() 上的一個動點,則
上的一個動點,則![]() 面積的最大值是_.
面積的最大值是_.
[問題解決]如圖2所示的是某街心花園的一角.在扇形![]() 中,
中,![]() 米,在圍墻
米,在圍墻![]() 和
和![]() 上分別有兩個入口
上分別有兩個入口![]() 和
和![]() 且
且![]() 米,
米,![]() 是
是![]() 的中點,出口
的中點,出口![]() 在
在![]() 上.現準備沿
上.現準備沿![]() 從入口到出口鋪設兩條景觀小路,在四邊形
從入口到出口鋪設兩條景觀小路,在四邊形![]() 內種花,在剩余區域種草.
內種花,在剩余區域種草.
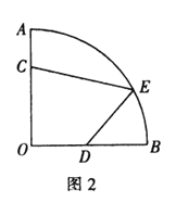
①出口![]() 設在距直線
設在距直線![]() 多遠處可以使四邊形
多遠處可以使四邊形![]() 的面積最大?最大面積是多少?(小路寬度不計)
的面積最大?最大面積是多少?(小路寬度不計)
②已知鋪設小路![]() 所用的普通石材每米的造價是
所用的普通石材每米的造價是![]() 元,鋪設小路
元,鋪設小路![]() 所用的景觀石材每米的造價是
所用的景觀石材每米的造價是![]() 元問:在
元問:在![]() 上是否存在點
上是否存在點![]() ,使鋪設小路
,使鋪設小路![]() 和
和![]() 的總造價最低?若存在,請求出最低總造價和出口
的總造價最低?若存在,請求出最低總造價和出口![]() 距直線
距直線![]() 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某斜拉橋引申出的部分平面圖,AE,CD是兩條拉索,其中拉索CD與水平橋面BE的夾角為72°,其底端與立柱AB底端的距離BD為4米,兩條拉索頂端距離AC為2米,若要使拉索AE與水平橋面的夾角為35°,請計算拉索AE的長.(結果精確到0.1米)(參考數據:sin35°≈![]() ,cos35°≈
,cos35°≈![]() ,tan35°≈
,tan35°≈![]() ,sin72°≈
,sin72°≈![]() ,cos72°≈
,cos72°≈![]() ,tan72°≈
,tan72°≈![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
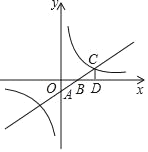
【題目】如圖,一次函數y=kx+b的圖象與坐標軸分別交于A、B兩點,與反比例函數y=![]() 的圖象在第一象限的交點為C,CD⊥x軸于D,若OB=3,OD=6,△AOB的面積為3.
的圖象在第一象限的交點為C,CD⊥x軸于D,若OB=3,OD=6,△AOB的面積為3.
(1)求一次函數與反比例函數的表達式;
(2)當x>0時,比較kx+b與![]() 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com