【題目】已知：
關于
的函數
的圖象與坐標軸只有兩個不同的交點
、
，
點坐標為
，則
的面積為_____．
【答案】1或
【解析】
根據k是否為0分類討論，當k=0時，求出點B和點A的坐標，利用待定系數法求出直線AP的解析式，即可求出AP與y軸交點C的坐標，然后根據S△PAB=S△ABC＋S△PBC即可求出結論；當k≠0時，根據題意可知拋物線與x軸只有一個交點，從而求出k的值，然后求出點B和點A的坐標，利用待定系數法求出直線AP的解析式，即可求出AP與y軸交點C的坐標，然后根據S△PAB=S△ABC＋S△PBC即可求出結論．
解：當k=0時，
設與x軸交于點A，與y軸交于點B，AP與y軸交于點C，則點A（-1，0），點B（0,1），過點P作PD⊥y軸于D，則PD=3，OA=1
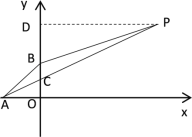
設直線AP的解析式為y=ax＋b
將點A和點P的坐標代入，得
解得：
∴直線AP的解析式為
將x=0代入，解得y=
∴點C的坐標為（0，）
∴BC=1－=
∴S△PAB=S△ABC＋S△PBC=BC·OA＋BC·PD=××1＋××3=1；
當k≠0時，
是
的二次函數，圖象必與y軸交于一點B（0，1）
∵
的圖象與坐標軸只有兩個不同的交點
、
，
∴
解得：
∴二次函數解析式為
將y=0代入，得
解得：x1=x2=-4
∴點A的坐標為（-4,0），即AO=4
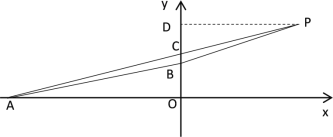
設直線AP的解析式為y=ax＋b
將點A和點P的坐標代入，得
解得：
∴直線AP的解析式為
將x=0代入，解得y=
∴點C的坐標為（0，）
∴BC=－1=
∴S△PAB=S△ABC＋S△PBC=BC·OA＋BC·PD=××4＋××3=；
綜上：S△PAB=1或
故答案為：1或．
科目：初中數學 來源： 題型：
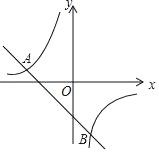
【題目】如圖，一次函數y1＝kx+b（k≠0）和反比例函數
的圖象相交于點A（﹣4，2），B（n，﹣4）
（1）求一次函數和反比例函數的表達式；
（2）觀察圖象，直接寫出不等式y1＜y2的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，已知拋物線
的頂點為
，與
軸的交點為
，
．
（1）求拋物線的解析式；
（2）M為軸上方拋物線上的一點，
與拋物線的對稱軸交于點
，若
，求點
的坐標；
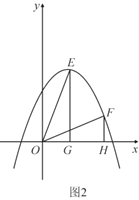
（3）如圖2，將原拋物線沿對稱軸平移后得到新拋物線為
，
，
是新拋物線在第一象限內互不重合的兩點，
軸，
軸，垂足分別為
，
，若始終存在這樣的點，，滿足
，求
的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
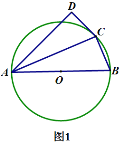
【題目】如圖1，
是
的外接，
是直徑，
是外一點且滿足
，連接
．
（1）求證：
是的切線；
（2）若
，
，
，求直徑的長；
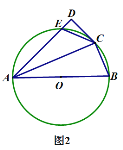
（3）如圖2，當
時，與交于
點，試寫出
、
、
之間的數量關系并證明．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知Rt△EBC中，∠B＝90°，A為BE邊上一點，以邊AC上的點O為圓心、OA為半徑的圓O與EC相切，D為切點，AD∥BC．
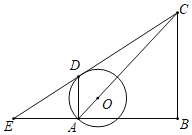
（1）求證：∠E＝∠ACB．
（2）若AD＝1，
，求BC的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
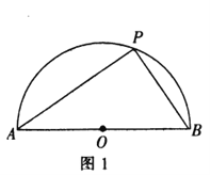
【題目】[問題發現]如圖1，半圓
的直徑
是半圓上的一個動點，則
面積的最大值是_．
[問題解決]如圖2所示的是某街心花園的一角．在扇形
中，
米，在圍墻
和
上分別有兩個入口
和
且
米，
是的中點，出口
在
上．現準備沿
從入口到出口鋪設兩條景觀小路，在四邊形
內種花，在剩余區域種草．
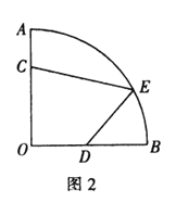
①出口設在距直線多遠處可以使四邊形的面積最大？最大面積是多少？（小路寬度不計）
②已知鋪設小路
所用的普通石材每米的造價是
元，鋪設小路
所用的景觀石材每米的造價是
元問：在上是否存在點，使鋪設小路和的總造價最低？若存在，請求出最低總造價和出口距直線的距離；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀以下材料，并按要求完成相應的任務：
萊昂哈德·歐拉（Leonhard Euler）是瑞士數學家，在數學上經常見到以他的名字命名的重要常數、公式和定理，下面是歐拉發現的一個定理：在△ABC 中，R 和 r 分別為外接圓和內切圓的半徑，O 和 I 分別為其外心和內心，則OI 
R2Rr .
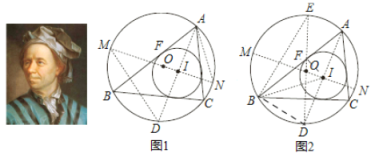
下面是該定理的證明過程（借助了第(2)問的結論）：
延長AI 交⊙O 于點 D，過點 I 作⊙O 的直徑 MN，連接 DM，AN.
∵∠D=∠N，∴∠DMI=∠NAI（同弧所對的圓周角相等），
∴△MDI∽△ANI.∴
，∴ IA ID IM IN ①
如圖②，在圖 1（隱去 MD，AN）的基礎上作⊙O 的直徑DE，連接BE，BD，BI，IF
∵DE 是⊙O 的直徑，∴∠DBE=90°.
∵⊙I 與 AB 相切于點 F，∴∠AFI=90°，
∴∠DBE=∠IFA.
∵∠BAD=∠E（同弧所對圓周角相等），
∴△AIF∽△EDB．
∴
，∴
②，
由（2）知：
，
∴
又∵
，
∴ 2Rr(R d )(R d ) ，
∴ R d 2Rr
∴ d R 2Rr
任務：（1）觀察發現： IM R d ， IN （用含R，d 的代數式表示）；
（2）請判斷 BD 和 ID 的數量關系，并說明理由.（請利用圖 1 證明）
（3）應用：若△ABC 的外接圓的半徑為 6cm，內切圓的半徑為 2cm，則△ABC 的外心與內心之間的距離為 cm．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：拋物線y＝a（x2﹣2mx﹣3m2）（m0）交x軸于A、B兩點（其中A點在B點左側），交y軸于點C．
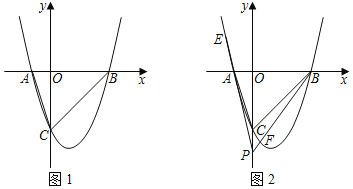
（1）若A點坐標為（﹣1，0），則B點坐標為 ．
（2）如圖1，在 （1）的條件下，且am＝1，設點M在y軸上且滿足∠OCA+∠AMO＝∠ABC，試求點M坐標．
（3）如圖2，在y軸上有一點P（0，n）（點P在點C的下方），直線PA、PB分別交拋物線于點E、F，若
，求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
