
 時,
時, ,2)中可以成為正方形ABCD的“等距圓”的圓心的是_______________;
,2)中可以成為正方形ABCD的“等距圓”的圓心的是_______________; 上,且⊙P是正方形ABCD的“等距圓”,則點P的坐標為_______________;
上,且⊙P是正方形ABCD的“等距圓”,則點P的坐標為_______________;
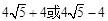 ;②
;② .
. ,
, ,
, .
. .
. .
.
 .
.

 口算能手系列答案
口算能手系列答案科目:初中數學 來源:不詳 題型:解答題
 ,四邊形ABCF的面積為S
,四邊形ABCF的面積為S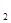 ,請直接寫出S
,請直接寫出S :S
:S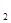 的值.
的值.
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 ,CF⊥BD分別交BD、AD于點E、F,連接BF.
,CF⊥BD分別交BD、AD于點E、F,連接BF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com