
【題目】如圖,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 邊的中點,點
邊的中點,點![]() 是正方形內一動點,
是正方形內一動點,![]() ,連接
,連接![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得
得![]() ,連接
,連接![]() ,
,![]() .
.
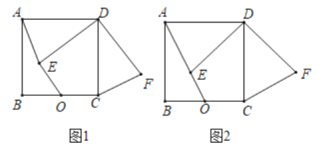
(1)如圖1,求證:![]() ;
;
(2)如圖2,若![]() ,
,![]() ,
,![]() 三點共線,求點
三點共線,求點![]() 到直線
到直線![]() 的距離.
的距離.
【答案】(1)證明見解析;(2)點F到直線BC的距離是![]() .
.
【解析】
(1)由旋轉的性質可得∠EDF=90°,DE=DF,由正方形的性質可得∠ADC=90°,DE=DF,可得∠ADE=∠CDF,由“SAS”可證△ADE≌△CDF,可得AE=CF;
(2)由勾股定理可求AO的長,可得AE=CF=3,通過證明△ABO∽△CPF,可得![]() ,即可求PF的長,即可求點F到直線BC的距離.
,即可求PF的長,即可求點F到直線BC的距離.
解:(1)由旋轉得:![]() ,
,![]() ,
,

∵四邊形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ;
;
(2)解:如圖2,過點F作FP⊥BC交BC延長線于點P,
則線段FP的長度就是點F到直線BC的距離.

∵點O是BC中點,且AB=BC=2![]()
∴BO=![]() ,
,
∴AO=![]() =5
=5
∵OE=2
∴AE=AO-OE=3
∵△ADE≌△CDF
∴AE=CF=3,∠DAO=∠DCF
∴∠BAO=∠FCP,且∠ABO=∠FPC=90°
∴△ABO∽△CPF
∴![]()
∴![]()
∴PF=![]()
∴點F到直線BC的距離為![]() .
.


 輕松暑假總復習系列答案
輕松暑假總復習系列答案科目:初中數學 來源: 題型:
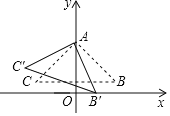
【題目】如圖,在Rt△ABC中,∠CAB=90°,AB=AC,點A在y軸上,BC∥x軸,點B![]() .將△ABC繞點A順時針旋轉的△AB′C′,當點B′落在x軸的正半軸上時,點C′的坐標為( )
.將△ABC繞點A順時針旋轉的△AB′C′,當點B′落在x軸的正半軸上時,點C′的坐標為( )
A.(﹣![]() ,
,![]() ﹣1)B.(﹣
﹣1)B.(﹣![]() ,
,![]() ﹣1)
﹣1)
C.(﹣![]() ,
,![]() +1)D.(﹣
+1)D.(﹣![]() ,
,![]() ﹣1)
﹣1)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,我們定義直線y=ax﹣a為拋物線y=ax2+bx+c(a、b、c為常數,a≠0)的“夢想直線”;有一個頂點在拋物線上,另有一個頂點在y軸上的三角形為其“夢想三角形”.
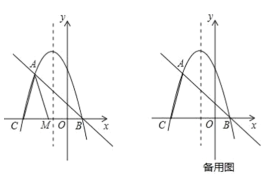
已知拋物線![]() 與其“夢想直線”交于A、B兩點(點A在點B的左側),與x軸負半軸交于點C.
與其“夢想直線”交于A、B兩點(點A在點B的左側),與x軸負半軸交于點C.
(1)填空:該拋物線的“夢想直線”的解析式為 ,
(2)如圖,點M為線段CB上一動點,將△ACM以AM所在直線為對稱軸翻折,點C的對稱點為N,若△AMN為該拋物線的“夢想三角形”,求點N的坐標;
(3)當點E在拋物線的對稱軸上運動時,在該拋物線的“夢想直線”上,是否存在點F,使得以點A、C、E、F為頂點的四邊形為平行四邊形?若存在,請直接寫出點E、F的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
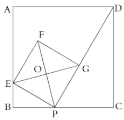
【題目】如圖,已知正方形![]() 的邊長為4,
的邊長為4,![]() 是邊
是邊![]() 上的一個動點,連接
上的一個動點,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() ,頂點
,頂點![]() 在線段
在線段![]() 上,對角線
上,對角線![]() ,
,![]() 相交于點
相交于點![]() .
.

(1)若![]() ,則
,則![]() ;
;
(2)①求證:點![]() 一定在
一定在![]() 的外接圓上;
的外接圓上;
②當點![]() 從點
從點![]() 運動到點
運動到點![]() 時,點
時,點![]() 也隨之運動,求點
也隨之運動,求點![]() 經過的路徑長;
經過的路徑長;
(3)在點![]() 從點
從點![]() 到點
到點![]() 的運動過程中,
的運動過程中,![]() 的外接圓的圓心也隨之運動,求該圓心到邊
的外接圓的圓心也隨之運動,求該圓心到邊![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某出租公司有若干輛同一型號的貨車對外出租,每輛貨車的日租金實行淡季、旺季兩種價格標準,旺季每輛貨車的日租金比淡季上漲![]() .據統計,淡季該公司平均每天有
.據統計,淡季該公司平均每天有![]() 輛貨車未出租,日租金總收入為
輛貨車未出租,日租金總收入為![]() 元;旺季所有的貨車每天能全部租出,日租金總收入為
元;旺季所有的貨車每天能全部租出,日租金總收入為![]() 元.
元.
(1)該出租公司這批對外出租的貨車共有多少輛?淡季每輛貨車的日租金多少元?
(2)經市場調查發現,在旺季如果每輛貨車的日租金每上漲![]() 元,每天租出去的貨車就會減少
元,每天租出去的貨車就會減少![]() 輛,不考慮其它因素,每輛貨車的日租金上漲多少元時,該出租公司的日租金總收入最高?
輛,不考慮其它因素,每輛貨車的日租金上漲多少元時,該出租公司的日租金總收入最高?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區在距離地面![]() 米的懸崖點
米的懸崖點![]() 處垂直水平線搭建了一個懸崖秋千,秋千拉繩均由鋼管制作而成,當游客乘坐該秋千時,機器會將秋千拉至最高接近與地面平行的點
處垂直水平線搭建了一個懸崖秋千,秋千拉繩均由鋼管制作而成,當游客乘坐該秋千時,機器會將秋千拉至最高接近與地面平行的點![]() 處(此時
處(此時![]() ) ,然后放下.該懸崖秋千以其驚險刺激立即成為網紅打卡地.
) ,然后放下.該懸崖秋千以其驚險刺激立即成為網紅打卡地.
![]() 若秋千放下
若秋千放下![]() 秒后
秒后![]() 點
點![]() 的垂直距離為
的垂直距離為![]() 米,求秋千拉繩
米,求秋千拉繩![]() 的長;
的長;
![]() 若某一時刻秋千蕩至與點
若某一時刻秋千蕩至與點![]() 水平距離相距
水平距離相距![]() 米的點
米的點![]() 處,求
處,求![]() 的度數,并求此時秋千底端距離懸崖底部多少米(結果保留整數參考數據:
的度數,并求此時秋千底端距離懸崖底部多少米(結果保留整數參考數據:![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
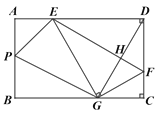
【題目】如圖,在矩形ABCD中,點E,F分別在邊AD,DC上,AB=6,DF=4,將矩形沿直線EF折疊,點D恰好落在BC邊上的點G處,連接DG交EF于點H.
(1)求DE的長度.
(2)求![]() 的值.
的值.
(3)若AB邊上有且只存在2個點P,使△APE與△BPG相似,請直接寫出邊AD的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將函數y=![]() (x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )
(x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com