【題目】邊長為4、中心為
的正方形
如圖所示，動點
從點
出發(fā)，沿
以每秒1個單位長度的速度運動到點時停止，動點
從點出發(fā)，沿
以每秒2個單位長度的速度運動一周停止，若點
同時開始運動，點的運動時間為
，當
時，滿足
的點的位置有（ ）
A.6個B.7個C.8個D.9個
【答案】B
【解析】
依次取
的中點
，連接
．由題意可知，當點
與點
到各自所在邊的中點的距離相等時，
，則有六種情況，分類列式計算求出t的值，即可解答本題．
解：依次取的中點，連接．
根據(jù)題意，得點運動的路程為
，當
時，點運動的路程為
．
分析題意可知，當點與點到各自所在邊的中點的距離相等時，．
當時，顯然
；
②當
時，如圖（1），點在
上，點在
上，
，
由
，得
；
③當
時，如圖（2），點在
上，點在
上，
，
由
，得
或
；
④當
時，如圖（3），點在
上，點在
上，
，
由
，得（舍去）或
；
⑤當
時，如圖（4），點在
上，點在
上，
，
由
，得
或
；
⑥當
時，點停在點
處，因此當
時，
，只有
時滿足
．
綜上，滿足條件
的點的位置有7個，
故選：B．
期末好成績系列答案
99加1領(lǐng)先期末特訓卷系列答案
百強名校期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案
金狀元績優(yōu)好卷系列答案科目：初中數(shù)學 來源： 題型：
【題目】某果品超市經(jīng)銷一種水果，已知該水果的進價為每千克15元，通過一段時間的銷售情況發(fā)現(xiàn)，該種水果每周的銷售總額相同，且每周的銷售量
(千克)與每千克售價
(元)的關(guān)系如表所示：
每千克售價 | 25 | 30 | 40 |
每周銷售量 | 240 | 200 | 150 |
（1）求出每周銷售量(千克)與每千克售價(元)的函數(shù)關(guān)系式．
（2）由于銷售淡季即將來臨，超市要完成每周銷售量不低于300千克的任務(wù)，則該種水果每千克售價最多定為多少元？
（3）在（2）的基礎(chǔ)上，超市銷售該種水果能否達到每周獲利2000元？說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】中考體育測評前，某校在初三15個班中隨機抽取了4個班的學生進行了摸底測評，將各班的滿分人數(shù)進行整理，繪制成如下兩幅統(tǒng)計圖．
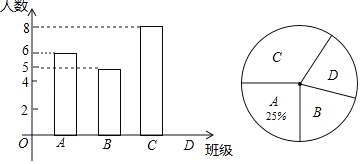
（1）D班滿分人數(shù)共 人，扇形統(tǒng)計圖中，表示C班滿分人數(shù)的扇形圓心角的度數(shù)為 ．
（2）這些滿分同學中有4名同學（3女1男）的跳繩動作十分標準，學校準備從這4名同學中任選2名同學作示范，請利用畫樹狀圖或列表法求選中1男1女的概率．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，拋物線
與
軸交于點
，與
軸交于點
，點
與點關(guān)于軸對稱，點
的坐標為
，過點作軸的垂線
交拋物線于點
．
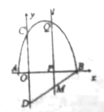
（1）求點
、點
、點的坐標；
（2）當點在線段
上運動時，直線交
于點
，試探究當
為何值時，四邊形
是平行四邊形；
（3）在點的運動過程中，是否存在點，使
是以為直角邊的直角三角形？若存在，求出點的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】有這樣一個問題探究函數(shù)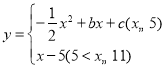
（b、c為常數(shù)）的圖象和性質(zhì)．元元根據(jù)學習函數(shù)的經(jīng)驗，對該函數(shù)的圖象和性質(zhì)進行了以下探究：
下面是元元的探究過程，請你補充完整
x | …… | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | …… |
y | …… | 0 | 2.5 | 4 | m | 4 | 2.5 | 0 | 1 | …… |
（1）根據(jù)上表信息，其中b＝____，c＝_____，m＝______．
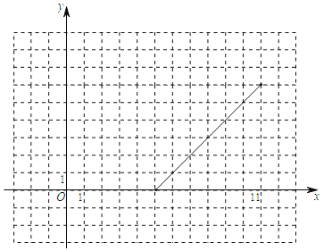
（2）如圖，在下面平面直角坐標系中，描出以補全后的表中各對應(yīng)值為坐標的點，并畫出該函數(shù)的另一部分圖象；
（3）觀察函數(shù)圖象，請寫出該函數(shù)的一條性質(zhì)：______．
（4）解決問題：若直線y＝3n+2（n為常數(shù)）與該函數(shù)圖象有3個交點時，求n的范圍．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
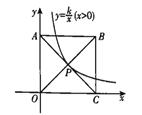
【題目】如圖，正方形OABC的兩邊在坐標軸上，頂點B落在第一象限，反比例函數(shù)
(x＞0)的圖象經(jīng)過正方形OABC的中心P，把反比例函數(shù)(x＞0)的圖象向左平移a個單位長度后經(jīng)過點A，若正方形OABC的邊長為4，則a的值為( )
A.
B.1C.
D.2
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
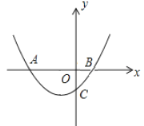
【題目】如圖，已知拋物線
交x軸于A(－4，0)，B兩點，交y軸于點C(0，－2)．
（1）求拋物線的解析式；
（2）過點M(m，0)(－4＜m＜0)且垂直于x軸的直線與拋物線相交于點N，求線段OM＋MN的最大值．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
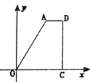
【題目】如圖，在四邊形
中，O為坐標原點，
在
軸上，
，
垂直于軸，
，
．若動點
、
同時從點0出發(fā)，點沿折線
運動，到達
點時停止；點沿運動，到達點時停止，它們運動的速度都是每秒1個單位長度。設(shè)運動秒時，
的面積為
（平方單位），則關(guān)于的函數(shù)圖象大致為（ ）
A.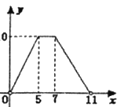
B.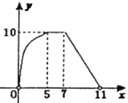
C.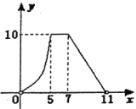
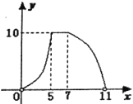
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
