
【題目】如圖,△ABC內(nèi)接于⊙O,BC=2,AB=AC,點D為![]() 上的動點,且cos∠ABC=
上的動點,且cos∠ABC=![]() .
.
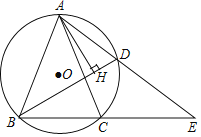
(1)求AB的長度;
(2)在點D的運動過程中,弦AD的延長線交BC延長線于點E,問ADAE的值是否變化?若不變,請求出ADAE的值;若變化,請說明理由;
(3)在點D的運動過程中,過A點作AH⊥BD,求證:BH=CD+DH.
【答案】(1)AB=![]() ;(2)不變,ADAE=10;(3)見解析
;(2)不變,ADAE=10;(3)見解析
【解析】
(1)作AM垂直于BC,由AB=AC,利用三線合一得到BM等于BC的一半,再由cos∠ABC的值,利用銳角三角函數(shù)定義求出AB的長即可;
(2)連接DC,由等邊對等角得到∠ACB=∠ABC,結(jié)合圓內(nèi)接四邊形的性質(zhì)得到∠ADC=∠ACE,然后證明△EAC∽△CAD,由相似得比例求出所求即可;
(3)在BD上取一點N,使得BN=CD,利用SAS得到△ABN≌△ACD,由全等三角形對應(yīng)邊相等和等腰三角形的性質(zhì)求出NH=HD即可得出結(jié)論.
解:(1)作AM⊥BC,
∵AB=AC,AM⊥BC,
∴BM=![]() BC=1,
BC=1,
∵cos∠ABC=![]() ,
,
∴AB=![]() ;
;
(2)連接DC,
由(1)知AB=AC=![]() ,
,
∴∠ACB=∠ABC,
∵四邊形ABCD內(nèi)接于圓O,
∴∠ADC+∠ABC=180°,
∵∠ACE+∠ACB=180°,
∴∠ADC=∠ACE,
∵∠CAE=∠DAC,
∴△EAC∽△CAD,
∴![]() ,
,
∴ADAE=AC2=10;
(3)在BD上取一點N,使得BN=CD,
在△ABN和△ACD中, ,
,
∴△ABN≌△ACD(SAS),
∴AN=AD,
∵AH⊥BD,
∴NH=HD,
∵BN=CD,NH=HD,
∴BN+NH=CD+HD,
即BH=CD+DH.



 初中暑期銜接系列答案
初中暑期銜接系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,二次函數(shù)![]() 的圖象與x軸交于點
的圖象與x軸交于點![]() 和點B,與y軸交于點
和點B,與y軸交于點![]() .
.
![]() 求該二次函數(shù)的表達式;
求該二次函數(shù)的表達式;
![]() 過點A的直線
過點A的直線![]() 且交拋物線于另一點D,求直線AD的函數(shù)表達式;
且交拋物線于另一點D,求直線AD的函數(shù)表達式;
![]() 在
在![]() 的條件下,在x軸上是否存在一點P,使得以B、C、P為頂點的三角形與
的條件下,在x軸上是否存在一點P,使得以B、C、P為頂點的三角形與![]() 相似?若存在,求出點P的坐標(biāo);若不存在,請說明理由.
相似?若存在,求出點P的坐標(biāo);若不存在,請說明理由.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,點
中,點![]() 為
為![]() 上一點,點
上一點,點![]() 為
為![]() 上一點,且
上一點,且![]() .
.
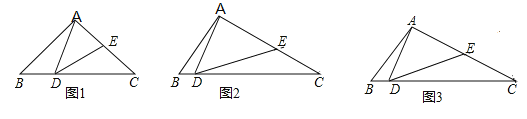
(1)如圖1,若![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,求證:
,求證:![]() ;
;
(3) 如圖3,在(2)的條件下,若![]() ,且
,且![]() ,
,![]() ,直接寫出線段
,直接寫出線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
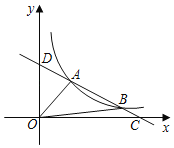
【題目】如圖,點A(m,3)、B(6,n)在雙曲線y=![]() (x>0)上,直線y=ax+b經(jīng)過A、B兩點,并與x軸、y軸分別相交手C、D兩點,已知S△OAB=8.
(x>0)上,直線y=ax+b經(jīng)過A、B兩點,并與x軸、y軸分別相交手C、D兩點,已知S△OAB=8.
(1)求雙曲線y=![]() 的函數(shù)表達式;
的函數(shù)表達式;
(2)求△COD的周長;
(3)直接寫出不等式![]() -ax>b的解集.
-ax>b的解集.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
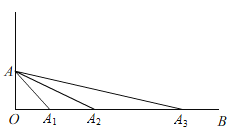
【題目】如圖,已知∠AOB=90°,點A繞點O順時針旋轉(zhuǎn)后的對應(yīng)點A1落在射線OB上,點A繞點A1順時針旋轉(zhuǎn)后的對應(yīng)點A2落在射線OB上,點A繞點A2順時針旋轉(zhuǎn)后的對應(yīng)點A3落在射線OB上,…,連接AA1,AA2,AA3…,依此作法,則∠AA2A3=___,∠AAnAn+1等于___度.(用含n的代數(shù)式表示,n為正整數(shù)).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“C919”大型客機首飛成功,激發(fā)了同學(xué)們對航空科技的興趣,如圖是某校航模興趣小組獲得的一張數(shù)據(jù)不完整的航模飛機機翼圖紙,圖中AB∥CD,AM∥BN∥ED,AE⊥DE,請根據(jù)圖中數(shù)據(jù),求出線段BE和CD的長.(sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,結(jié)果保留小數(shù)點后一位)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
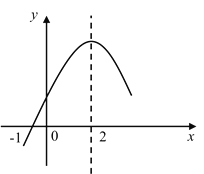
【題目】二次函數(shù)y=ax2+bx+c(a≠0)的部分圖象如圖所示,圖象過點(﹣1,0),對稱軸為直線x=2,下列結(jié)論:①4a+b=0;②9a+c>3b;③ 8a+7b+2c>0;④若點A(﹣3,y1)、點B(![]() ,y2)、點C(
,y2)、點C(![]() ,y3)在該函數(shù)圖象上,則y1<y3<y2;⑤若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結(jié)論有_______個.
,y3)在該函數(shù)圖象上,則y1<y3<y2;⑤若方程a(x+1)(x﹣5)=﹣3的兩根為x1和x2,且x1<x2,則x1<﹣1<5<x2.其中正確的結(jié)論有_______個.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,△ABC中,∠C=90°,BC=8cm,AC:AB=3:5,點P從點B出發(fā)沿BC向點C以2cm/s的速度移動,點Q從點C出發(fā)沿CA向點A以1cm/s的速度移動,如果P、Q分別從B、C同時出發(fā):
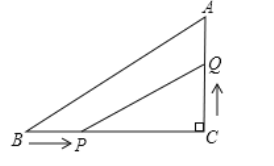
(1)經(jīng)過多少秒后,△CPQ的面積為8cm?
(2)經(jīng)過多少秒時,以C、P、Q為頂點的三角形恰與△ABC相似?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
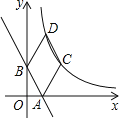
【題目】如圖,直線y=ax+2與x軸交于點A(1,0),與y軸交于點B(0,b).將線段AB先向右平移1個單位長度,再向上平移t(t>0)個單位長度,得到對應(yīng)線段CD,反比例函數(shù)y=![]() (x>0)的圖象恰好經(jīng)過C、D兩點,連接AC、BD.
(x>0)的圖象恰好經(jīng)過C、D兩點,連接AC、BD.
(1)請直接寫出a和b的值;
(2)求反比例函數(shù)的表達式及四邊形ABDC的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com