
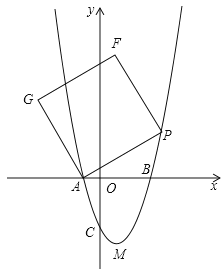
【題目】如圖,在平面直角坐標系xoy中,把拋物線![]() 先向右平移1個單位,再向下平移4個單位,得到拋物線
先向右平移1個單位,再向下平移4個單位,得到拋物線![]() ,所得拋物線與x軸交于A、B兩點
,所得拋物線與x軸交于A、B兩點![]() 點A在點B的左邊
點A在點B的左邊![]() ,與y軸交于點C,頂點為M;
,與y軸交于點C,頂點為M;
![]() 寫出h、k的值以及點A、B的坐標;
寫出h、k的值以及點A、B的坐標;
![]() 判斷三角形BCM的形狀,并計算其面積;
判斷三角形BCM的形狀,并計算其面積;
![]() 點P是拋物線上一動點,在y軸上找點
點P是拋物線上一動點,在y軸上找點![]() 使點A,B,P,Q組成的四邊形是平行四邊形,直接寫出對應的點P的坐標
使點A,B,P,Q組成的四邊形是平行四邊形,直接寫出對應的點P的坐標![]() 不用寫過程
不用寫過程![]()
![]() 點P是拋物線上一動點,連接AP,以AP為一邊作正方形APFG,隨著點P的運動,正方形的大小、位置也隨之改變
點P是拋物線上一動點,連接AP,以AP為一邊作正方形APFG,隨著點P的運動,正方形的大小、位置也隨之改變![]() 當頂點F或G恰好落在y軸上時,請直接寫出對應的點P的坐標
當頂點F或G恰好落在y軸上時,請直接寫出對應的點P的坐標![]() 不寫過程
不寫過程![]()
![]()
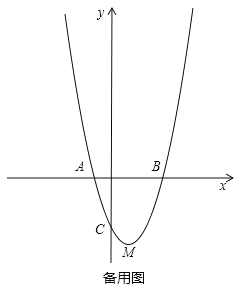
【答案】(1)![]() ,B
,B![]() ;(2)3;(3)點P的坐標為
;(2)3;(3)點P的坐標為![]() ,
,![]() 或
或![]() ;(4)
;(4)![]() ,
,![]() ,
,![]() 或
或![]()
【解析】
![]() 利用拋物線的平移規律即可求得h和k的值;然后令
利用拋物線的平移規律即可求得h和k的值;然后令![]() 即可求得與x軸的交點坐標;
即可求得與x軸的交點坐標;
![]() 首先求得點C和點M的坐標,然后求得BC、CM及BM的長,最后利用勾股定理逆定理判定直角三角形即可;
首先求得點C和點M的坐標,然后求得BC、CM及BM的長,最后利用勾股定理逆定理判定直角三角形即可;
![]() 分兩AB為邊和AB為對角線兩種情況討論計算即可.
分兩AB為邊和AB為對角線兩種情況討論計算即可.
![]() 分別根據當點G在y軸上時和點F在y軸上時兩種情況利用
分別根據當點G在y軸上時和點F在y軸上時兩種情況利用![]() ≌
≌![]() 和
和![]() ≌
≌![]() 求得點P的坐標即可.
求得點P的坐標即可.
![]() 拋物線
拋物線![]() 先向右平移1個單位,再向下平移4個單位,得到拋物線
先向右平移1個單位,再向下平移4個單位,得到拋物線![]() ,
,
![]() ,
,![]() ;
;
令![]() ,即
,即![]()
解得![]() 或
或![]() ,
,
![]() ,B
,B![]() ,
,
![]() 令
令![]() ,得
,得![]() ,
,
![]() 點C的坐標為
點C的坐標為![]() ,點M的坐標為
,點M的坐標為![]()
![]() ,
,![]() ,
,![]()
![]()
![]() 是直角三角形;
是直角三角形;
![]() ;
;
![]() 由
由![]() 知,拋物線
知,拋物線![]() ,
,
![]() 點P是拋物線上一動點,
點P是拋物線上一動點,
![]() 設
設![]() ,
,
![]() 點Q在y軸上,
點Q在y軸上,
![]() 設
設![]() ,
,
![]() ,
,![]() ,
,
![]() ,AB的中點
,AB的中點![]()
![]() 點A,B,P,Q組成的四邊形是平行四邊形,
點A,B,P,Q組成的四邊形是平行四邊形,
![]() 當AB為邊時,
當AB為邊時,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
Ⅰ、當![]() 時,
時,![]() ,
,
![]() ,
,
Ⅱ、當![]() 時,
時,![]() ,
,
![]()
![]() 當AB為對角線時,點M是PQ的中點,
當AB為對角線時,點M是PQ的中點,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 點P的坐標為
點P的坐標為![]() ,
,![]() 或
或![]() ,
,
![]() 如圖
如圖![]() ,
,![]() 當點G在y軸上時,
當點G在y軸上時,


由![]() ≌
≌![]() ,
,
得![]() ,得
,得![]() ,
,
![]() ,
,
得![]() ,
,
![]() ,
,![]()
![]() 如圖
如圖![]() ,
,

當點F在y軸上時,由![]() ≌
≌![]() ,
,
得![]() ,得
,得![]() ,
,
則![]() ,
,
得![]() ,
,![]()
故![]() 或
或![]()


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,點D,E,F分別在AB,BC,AC邊上,且BE=CF,BD=CE.
(1)求證:△DEF是等腰三角形;
(2)當∠A=50°時,求∠DEF的度數;
(3)若∠A=∠DEF,判斷△DEF是否為等腰直角三角形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王抽樣調查了本地若干天的空氣質量情況,把空氣質量分成四類:![]() 類,
類,![]() 類,
類,![]() 類和
類和![]() 類,分別對應的質量級別為優、良、輕度污染和中度污染四種情況,并繪制兩個統計圖(部分信息缺失);
類,分別對應的質量級別為優、良、輕度污染和中度污染四種情況,并繪制兩個統計圖(部分信息缺失);
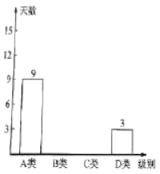
空氣質量條形統計圖
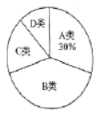
空氣質量扇形統計圖
(1)本次調查的樣本容量是________;
(2)已知![]() 類和
類和![]() 類在扇形統計圖中所占的夾角為
類在扇形統計圖中所占的夾角為![]() 度,
度,![]() 類的頻數是
類的頻數是![]() 類的
類的![]() 倍,通過計算,求出
倍,通過計算,求出![]() 類和
類和![]() 類的頻數,并完成條形統計圖;
類的頻數,并完成條形統計圖;
(3)計算![]() 類在扇形統計圖中所對應的圓心角度數;
類在扇形統計圖中所對應的圓心角度數;
(4)若一年按![]() 天計算,求本地全年空氣質量達到優良以上的天數(保留整數).
天計算,求本地全年空氣質量達到優良以上的天數(保留整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() ,點B在x軸上,且
,點B在x軸上,且![]() .
.
![]() 求點B的坐標;
求點B的坐標;
![]() 求
求![]() 的面積;
的面積;
![]() 在y軸上是否存在P,使以A、B、P三點為頂點的三角形的面積為10?若存在,請求出點P的坐標;若不存在,請說明理由.
在y軸上是否存在P,使以A、B、P三點為頂點的三角形的面積為10?若存在,請求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
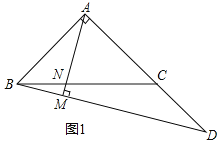
【題目】如圖,在![]() 中,
中,![]() ,點D為AC延長線上一點,連接BD,過A作
,點D為AC延長線上一點,連接BD,過A作![]() ,垂足為M,交BC于點N
,垂足為M,交BC于點N
![]() 如圖1,若
如圖1,若![]() ,
,![]() ,求AM的長;
,求AM的長;
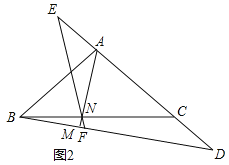
![]() 如圖2,點E在CA的延長線上,且
如圖2,點E在CA的延長線上,且![]() ,連接EN并延長交BD于點F,求證:
,連接EN并延長交BD于點F,求證:![]() ;
;
![]() 在
在![]() 的條件下,當
的條件下,當![]() 時,請求出
時,請求出![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將函數y=![]() (x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )
(x﹣2)2+1的圖象沿y軸向上平移得到一條新函數的圖象,其中點A(1,m),B(4,n)平移后的對應點分別為點A'、B'.若曲線段AB掃過的面積為9(圖中的陰影部分),則新圖象的函數表達式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=ax+b的圖象與反比例函數![]() 的圖象交于C,D兩點,與x,y軸交于B,A兩點,且tan∠ABO=
的圖象交于C,D兩點,與x,y軸交于B,A兩點,且tan∠ABO=![]() ,OB=4,OE=2.
,OB=4,OE=2.
(1)求一次函數的解析式和反比例函數的解析式;
(2)求△OCD的面積;
(3)根據圖象直接寫出一次函數的值大于反比例函數的值時,自變量x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】騰飛中學在教學樓前新建了一座“騰飛”雕塑(如圖①).為了測量雕塑的高度,小明在二樓找到一點C,利用三角板測得雕塑頂端A點的仰角為![]() ,底部B點的俯角為
,底部B點的俯角為![]() ,小華在五樓找到一點D,利用三角板測得A點的俯角為
,小華在五樓找到一點D,利用三角板測得A點的俯角為![]() (如圖②).若已知CD為10米,請求出雕塑AB的高度.(結果精確到0.1米,參考數據
(如圖②).若已知CD為10米,請求出雕塑AB的高度.(結果精確到0.1米,參考數據![]() ).
).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,每個小正方形的邊長均為1個單位長度,△ABC的三個頂點的位置如圖所示,現將△ABC平移,使點A變換為點A',點B'、C'分別是B、C的對應點.
(1)請畫出平移后的△A'B'C',并求△A'B'C'的面積= ;
(2)請在AB上找一點P,使得線段CP平分△ABC的面積,在圖上作出線段CP;
(3)請在圖中畫出過點C且平行于AB的直線CM.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com