
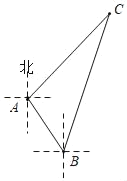
【題目】如圖,某考察船在某海域進行科考活動,在點A測得小島C在它的東北方向上,它沿南偏東37°方向航行了2海里到達點B處,又測得小島C在它的北偏東23°方向上.
(1)求∠C的度數;
(2)求該考察船在點B處與小島C之間的距離.(精確到0.1海里)
(參考數據:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
【答案】(1)22°;(2)5.25.
【解析】
(1)由已知方位角,根據平行線的性質、角的和差關系及三角形的內角和定理可得∠CAB、∠ABC、∠C的度數.
(2)過點A作AM⊥BC,構造直角△ABM和直角△CAM,利用直角三角形的邊角關系,可求出線段AM、CM、BM的長,從而問題得解.
解:(1)過點A作AM⊥BC,垂足為M.
由題意知:AB=2海里,∠NAC=∠CAE=45°,
∠SAB=37°,∠DBC=23°,
∵∠SAB=37°,DB∥AS,
∴∠DBA=37°,∠EAB=90°﹣∠SAB=53°.
∴∠ABC=∠ABD+∠DBC=37°+23°=60°,
∠CAB=∠EAB+∠CAE=53°+45°=98°.
∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣98°﹣60°=22°.
(2)在Rt△AMB中,∵AB=2海里,∠ABC=60°,
∴BM=1海里,AM=![]() 海里.
海里.
在Rt△AMC中,tanC=![]() ,
,
∴CM=![]() =4.25(海里)
=4.25(海里)
∴CB=CM+BM=4.25+1=5.25(海里)
答:考察船在點B處與小島C之間的距離為5.25海里.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案 ABC考王全優卷系列答案
ABC考王全優卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD內接于⊙O,BD是⊙O的直徑,AE⊥CD于點E,DA平分∠BDE.
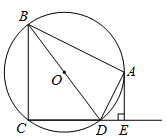
(1)求證:AE是⊙O的切線;
(2)如果AB=4,AE=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店為了迎接“讀書節”制定了活動計劃,以下是活動計劃書的部分信息:
“讀書節”活動計劃書 | ||
書本類別 | A類 | B類 |
進價(單位:元) | 18 | 12 |
備注 | 1.用不超過16800元購進A,B兩類圖書共1000本; 2.A類圖書不少于600本; …… |
(1)陳經理查看計劃數時發現:A類圖書的標價是B類圖書標價的1.5倍,若顧客用540元購買圖書,能單獨購買A類圖書的數量恰好比單獨購買B類圖書的數量少10本,請求出A,B兩類圖書的標價;
(2)經市場調查后,陳經理發現他們高估了“讀書節”對圖書銷售的影響,便調整了銷售方案,A類圖書每本標價降低a元(0<a<5)銷售,B類圖書價格不變,那么書店應如何進貨才能獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某飾品店老板去批發市場購買新款手鏈,第一次購手鏈共用1000元,將該手鏈以每條定價28元銷售,并很快售完,所得利潤率高于30%.由于該手鏈深得年輕人喜愛,十分暢銷,第二次去購進手鏈時,每條的批發價已比第一次高5元,共用去了1500元,所購數量比第一次多10條.當這批手鏈以每條定價32元售出80%時,出現滯銷,便以5折價格售完剩余的手鏈.現假設第一次購進手鏈的批發價為x元/條.
(1)用含x的代數式表示:第一次購進手鏈的數量為 條;
(2)求x的值;
(3)不考慮其他因素情況下,試問該老板第二次售手鏈是賠錢了,還是賺錢了?若賠錢,賠多少?若賺錢,賺多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將矩形ABCD繞點B順時針旋轉得到矩形A1BC1D1,點A、C、D的對應點分別為A1、C1、D1.
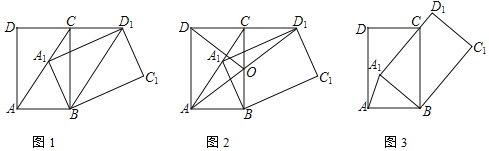
(1)當點A1落在AC上時:
①如圖1,若∠CAB=60°,求證:四邊形ABD1C為平行四邊形;
②如圖2,AD1交CB于點O,若∠CAB≠60°,求證:DO=AO;
(2)如圖3,當A1D1過點C時,若BC=10,CD=6,直接寫出A1A的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
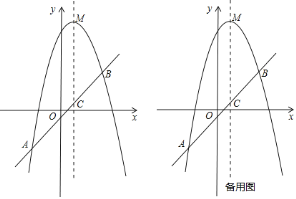
【題目】已知,如圖,拋物線![]() 的頂點為
的頂點為![]() ,經過拋物線上的兩點
,經過拋物線上的兩點![]() 和
和![]() 的直線交拋物線的對稱軸于點
的直線交拋物線的對稱軸于點![]() .
.
(1)求拋物線的解析式和直線![]() 的解析式.
的解析式.
(2)在拋物線上![]() 兩點之間的部分(不包含
兩點之間的部分(不包含![]() 兩點),是否存在點
兩點),是否存在點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)若點![]() 在拋物線上,點
在拋物線上,點![]() 在
在![]() 軸上,當以點
軸上,當以點![]() 為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點
為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在線段![]() 上任取一點
上任取一點![]() ,將線段
,將線段![]() 逆時針旋轉
逆時針旋轉![]() 得到線段
得到線段![]() ,將線段
,將線段![]() 順時針旋轉
順時針旋轉![]() 得到線段
得到線段![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,連接
的中點,連接![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 交
交![]() 于點
于點![]() .直線
.直線![]() 分別交
分別交![]() ,
,![]() 于
于![]() ,
,![]() 兩點,有下列結論:①
兩點,有下列結論:①![]() ;②四邊形
;②四邊形![]() 為平行四邊形;③
為平行四邊形;③![]() ;④
;④![]() .其中正確的結論是( )
.其中正確的結論是( )
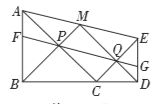
A.①③④B.①②③C.②③④D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩:我問開店李三公,眾客都來到店中,一房七客多七客,一房九客一房空.詩中后兩句的意思是:如果每一間客房住7人,那么有7人無房可住;如果每一間客房住9人,那么就空出一間房.
(1)求該店有客房多少間?房客多少人?
(2)假設店主李三公將客房進行改造后,房間數大大增加.每間客房收費20錢,且每間客房最多入住4人,一次性定客房18間以上(含18間),房費按8折優惠.若詩中“眾客”再次一起入住,他們如何訂房更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y1=﹣x+4,y2=![]() x+b都與雙曲線y=
x+b都與雙曲線y=![]() 交于點A(1,m),這兩條直線分別與x軸交于B,C兩點.
交于點A(1,m),這兩條直線分別與x軸交于B,C兩點.
(1)求y與x之間的函數關系式;
(2)直接寫出當x>0時,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若點P在x軸上,連接AP把△ABC的面積分成1:3兩部分,求此時點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com