【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩：我問開店李三公，眾客都來到店中，一房七客多七客，一房九客一房空．詩中后兩句的意思是：如果每一間客房住7人，那么有7人無房可住；如果每一間客房住9人，那么就空出一間房．
（1）求該店有客房多少間？房客多少人？
（2）假設店主李三公將客房進行改造后，房間數大大增加．每間客房收費20錢，且每間客房最多入住4人，一次性定客房18間以上（含18間），房費按8折優惠．若詩中“眾客”再次一起入住，他們如何訂房更合算？
【答案】（1）該店有客房8間，房客63人；（2）詩中“眾客”再次一起入住，他們應選擇一次性訂房18間更合算．
【解析】（1）設該店有客房x間，房客y人；根據題意得出方程組，解方程組即可；
（2）根據題意計算：若每間客房住4人，則63名客人至少需客房16間，求出所需付費；若一次性定客房18間，求出所需付費，進行比較，即可得出結論．
解：（1）設該店有客房x間，房客y人；
根據題意得：
，解得：
．
答：該店有客房8間，房客63人；
（2）若每間客房住4人，則63名客人至少需客房16間，需付費20×16=320錢
若一次性定客房18間，則需付費20×18×0.8=288千＜320錢；
答：詩中“眾客”再次一起入住，他們應選擇一次性訂房18間更合算．
“點睛”本題考查了二元一次方程組的應用；根據題意得出方程組是解決問題的關鍵．
開心練習課課練與單元檢測系列答案
開心試卷期末沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】計算:
(1) (－4x2y)·(－x2y2)·(
y)3； (2) (－3ab)(2a2b＋ab－1) ；
(3) (m－
)(m＋
)； （4） （-x-1）(-x+1) ； (5) ( - x - 5)2 ； （6）
；
（7）先化簡，再求值：（x+1）2﹣（x+2）（x﹣2），其中
；
(8)解方程組
.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在
中， 
， 
，點
在
的延長線上， 
是
的中點， 
是射線
上一動點，且
，連接
，作
， 
交
延長線于點
．
（
）如圖
，當點
在
上時，填空： 
__________ 
（填“
”、“
”或“
”）．
（
）如圖
，當點
在
的延長線上時，請根據題意將圖形補全，判斷
與
的數量關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果一個實際問題的函數圖象的形狀與y= 
的形狀相同，且頂點坐標是(4，－2)，那么它的函數解析式為( )．
A.y= 
B.y= 或y= 
C.y= 
D.y= 或y=
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】杭州休博會期間，嘉年華游樂場投資150萬元引進一項大型游樂設施．若不計維修保養費用，預計開放后每月可創收33萬元．而該游樂設施開放后，從第1個月到第x個月的維修保養費用累計為y（萬元），且y=ax2+bx；若將創收扣除投資和維修保養費用稱為游樂場的純收益g（萬元），g也是關于x的二次函數；
（1）若維修保養費用第1個月為2萬元，第2個月為4萬元．求y關于x的解析式；
（2）求純收益g關于x的解析式；
（3）問設施開放幾個月后，游樂場的純收益達到最大；幾個月后，能收回投資？
查看答案和解析>>
科目：初中數學 來源： 題型：
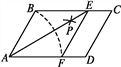
【題目】如圖,在ABCD中,以點A為圓心,AB長為半徑畫弧交AD于點F,再分別以點B,F為圓心,大于BF的相同長為半徑畫弧,兩弧交于點P;連接AP并延長交BC于點E,連接EF,則所得四邊形ABEF是菱形.
(1)根據以上尺規作圖的過程,求證:四邊形ABEF是菱形;
(2)若菱形ABEF的周長為16,AE=
,求∠C的大小.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于二次函數y=x2-2mx-3 ， 有下列說法：
①它的圖象與x軸有兩個公共點；
②如果當x≤1時y隨x的增大而減小，則m=1；
③如果將它的圖象向左平移3個單位后過原點，則m=-1；
④如果當x=4時的函數值與x=2008時的函數值相等，則當x=2012時的函數值為-3 ．
其中正確的說法是 ． （把你認為正確說法的序號都填上）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
