Question

【題目】如圖，在矩形中，，動點從點出發(fā)，沿射線以每秒個單位的速度向點方向運動，連接，把沿翻折，得到．設點的運動時間為．

（1）若，當三點在同一直線上時，求的值；

（2）若點到直線的距離等于，求的值；

（3）若的最小值為，直接寫出的值．

Answer 1

【答案】（1）t=3 -；（2）t= ；（3）m= ．

【解析】

（1）如圖1中，設PD=t．則PA=3-t．首先證明BP=BC=6，在Rt△ABP中利用勾股定理即可解決問題；

（2）通過添加輔助線，構造直角三角形再解決問題；

（3）當點A,點E，點C在同一條直線上時，AE最短，利用勾股定理求值即可．

解：（1）如圖1中，設PD=t．則PA=3-t

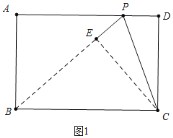
∵P、B、E共線，
∴∠BPC=∠DPC，
∵AD∥BC，
∴∠DPC=∠PCB，
∴∠BPC=∠PCB，
∴BP=BC=3，
在Rt△ABP中，

∵AB2+AP2=BP2，
∴22+（3-t）2=32，
∴t=3 +（舍去）或3-

∴當t=3 -時，三點在同一直線上．

（2） 過點E作MN⊥BC，交AD于點M

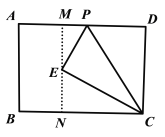
∵四邊形ABCD是矩形，MN⊥BC

∴MN⊥AD

∵點到直線的距離等于

∴EN=1

∵MN=AB=2, EC=CD=2,

∴EN=MN-EN=2-1=1

∴在Rt△ENC中，NC=

∴MD= NC=

∵由題意得：MP=MD-PD=-t,ME=MN-EN=2-1=1,EP=PD=t

∴在Rt△MPE中，

即：，解得：t=

（3）如圖，當點A,點E，點C在同一條直線上時，AE最短．

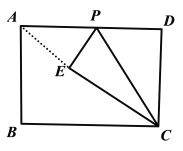
由題意得：=，EC=CD=AB=2

∴在Rt△ABC中，

∴m=AD=BC=．