
【題目】如圖,正方形![]() 中,點(diǎn)
中,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā)沿
出發(fā)沿![]() 邊向點(diǎn)
邊向點(diǎn)![]() 運(yùn)動,到達(dá)點(diǎn)
運(yùn)動,到達(dá)點(diǎn)![]() 停止.作射線
停止.作射線![]() ,將
,將![]() 繞著點(diǎn)
繞著點(diǎn)![]() 逆時針旋轉(zhuǎn)45°,與
逆時針旋轉(zhuǎn)45°,與![]() 邊交于點(diǎn)
邊交于點(diǎn)![]() ,連接
,連接![]() .
.
(1)畫圖,完善圖形.
(2)三條線段![]() ,
,![]() ,
,![]() 之間有無確定的數(shù)量關(guān)系?請說明理由.
之間有無確定的數(shù)量關(guān)系?請說明理由.
(3)過點(diǎn)![]() 作
作![]() 于
于![]() .若線段
.若線段![]() 的最大值為4,求點(diǎn)
的最大值為4,求點(diǎn)![]() 運(yùn)動的路徑長.
運(yùn)動的路徑長.
【答案】(1)見解析;(2)![]() ,理由見解析;(3)
,理由見解析;(3)![]()
【解析】
(1)依題意補(bǔ)全圖形即可;
(2將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)90°到
逆時針旋轉(zhuǎn)90°到![]() ,
,![]() ,得出
,得出![]() ,
,![]() .證明
.證明![]() ,得出
,得出![]() ,即可得出結(jié)論;
,即可得出結(jié)論;
(3)確定點(diǎn)H的運(yùn)動軌跡,利用弧長公式計算即可.
解:(1)畫圖,如圖所示:
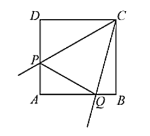
(2)![]() ,
,![]() ,
,![]() 之間有確定的數(shù)量關(guān)系,
之間有確定的數(shù)量關(guān)系,![]() .
.
理由如下.
如圖1,
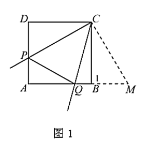
∵![]() 是正方形,
是正方形,
∴可將![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)90°到
逆時針旋轉(zhuǎn)90°到![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() .
.
∴Q,B,M在同一條直線上.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
(3)如圖2,
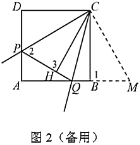
由(2),![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
當(dāng)點(diǎn)![]() 還在點(diǎn)
還在點(diǎn)![]() 處時,
處時,![]() 是正方形的對角線,此時最長,
是正方形的對角線,此時最長,
即正方形的對角線為4.
∴正方形的邊長![]() ,
,
∴![]() ,
,
當(dāng)點(diǎn)![]() 從
從![]() 到點(diǎn)
到點(diǎn)![]() 時,點(diǎn)
時,點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 沿圓弧到點(diǎn)
沿圓弧到點(diǎn)![]() ,圓心角
,圓心角![]() .
.
∴點(diǎn)![]() 運(yùn)動的路徑長為
運(yùn)動的路徑長為![]() .
.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知二次函數(shù)y=ax2+bx﹣3a經(jīng)過點(diǎn)A(﹣1,0)、C(0,3),與x軸交于另一點(diǎn)B,拋物線的頂點(diǎn)為D.

(1)求此二次函數(shù)解析式;
(2)連接DC、BC、DB,求證:△BCD是直角三角形;
(3)在對稱軸右側(cè)的拋物線上是否存在點(diǎn)P,使得△PDC為等腰三角形?若存在,求出符合條件的點(diǎn)P的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】問題探究,
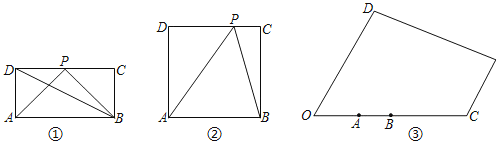
(1)如圖①,在矩形ABCD中,AB=2AD,P為CD邊上的中點(diǎn),試比較∠APB和∠ADB的大小關(guān)系,并說明理由;
(2)如圖②,在正方形ABCD中,P為CD上任意一點(diǎn),試問當(dāng)P點(diǎn)位于何處時∠APB最大?并說明理由;
問題解決
(3)某兒童游樂場的平面圖如圖③所示,場所工作人員想在OD邊上點(diǎn)P處安裝監(jiān)控裝置,用來監(jiān)控OC邊上的AB段,為了讓監(jiān)控效果最佳,必須要求∠APB最大,已知:∠DOC=60°,OA=400米,AB=200![]() 米,問在OD邊上是否存在一點(diǎn)P,使得∠APB最大,若存在,請求出此時OP的長和∠APB的度數(shù);若不存在,請說明理由.
米,問在OD邊上是否存在一點(diǎn)P,使得∠APB最大,若存在,請求出此時OP的長和∠APB的度數(shù);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,兩張等寬的紙條交叉疊放在一起,若重疊都分構(gòu)成的四邊形ABCD中,AB=3,BD=4.則AC的長為_________________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】定義:我們把對角線互相垂直的四邊形叫做神奇四邊形.順次連接四邊形各邊中點(diǎn)得到的四邊形叫做中點(diǎn)四邊形.
(1)判斷:
①在平行四邊形、矩形、菱形中,一定是神奇四邊形的是 ;
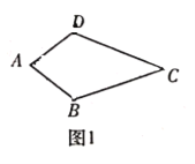
②命題:如圖1,在四邊形![]() 中,
中,![]() 則四邊形
則四邊形![]() 是神奇四邊形.此命題是_____(填“真”或“假”)命題;
是神奇四邊形.此命題是_____(填“真”或“假”)命題;
③神奇四邊形的中點(diǎn)四邊形是
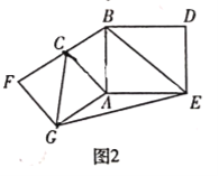
(2)如圖2,分別以![]() 的直角邊
的直角邊![]() 和斜邊
和斜邊![]() 為邊向外作正方形
為邊向外作正方形![]() 和正方形
和正方形![]() ,連接
,連接![]()
①求證:四邊形![]() 是神奇四邊形;
是神奇四邊形;
②若![]() ,求
,求![]() 的長;
的長;
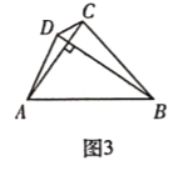
(3)如圖3,四邊形![]() 是神奇四邊形,若
是神奇四邊形,若![]() 分別是方程
分別是方程![]() 的兩根,求
的兩根,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“揚(yáng)州漆器”名揚(yáng)天下,某網(wǎng)店專門銷售某種品牌的漆器筆筒,成本為30元/件,每天銷售量![]() (件)與銷售單價
(件)與銷售單價![]() (元)之間存在一次函數(shù)關(guān)系,如圖所示.
(元)之間存在一次函數(shù)關(guān)系,如圖所示.

(1)求![]() 與
與![]() 之間的函數(shù)關(guān)系式;
之間的函數(shù)關(guān)系式;
(2)如果規(guī)定每天漆器筆筒的銷售量不低于240件,當(dāng)銷售單價為多少元時,每天獲取的利潤最大,最大利潤是多少?
(3)該網(wǎng)店店主熱心公益事業(yè),決定從每天的銷售利潤中捐出150元給希望工程,為了保證捐款后每天剩余利潤不低于3600元,試確定該漆器筆筒銷售單價的范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】龍人文教用品商店欲購進(jìn)![]() 、
、![]() 兩種筆記本,用160元購進(jìn)的
兩種筆記本,用160元購進(jìn)的![]() 種筆記本與用240元購進(jìn)的
種筆記本與用240元購進(jìn)的![]() 種筆記本數(shù)量相同,每本
種筆記本數(shù)量相同,每本![]() 種筆記本的進(jìn)價比每本
種筆記本的進(jìn)價比每本![]() 種筆記本的進(jìn)價貴10元.
種筆記本的進(jìn)價貴10元.
(1)求![]() 、
、![]() 兩種筆記本每本的進(jìn)價分別為多少元?
兩種筆記本每本的進(jìn)價分別為多少元?
(2)若該商店準(zhǔn)備購進(jìn)![]() 、
、![]() 兩種筆記本共100本,且購買這兩種筆記本的總價不超過2650元,則至少購進(jìn)
兩種筆記本共100本,且購買這兩種筆記本的總價不超過2650元,則至少購進(jìn)![]() 種筆記本多少本?
種筆記本多少本?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
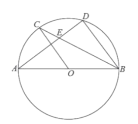
【題目】如圖,![]() 為⊙
為⊙![]() 的直徑,
的直徑,![]() ,
,![]() 為圓上的兩點(diǎn),
為圓上的兩點(diǎn),![]() ,弦
,弦![]() ,
,![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,
,
(1)求證:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半徑;
的半徑;
(3)在(2)的條件下,過點(diǎn)![]() 作⊙
作⊙![]() 的切線,交
的切線,交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 兩點(diǎn)(點(diǎn)
兩點(diǎn)(點(diǎn)![]() 在線段
在線段![]() 上),求
上),求![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】按要求作圖,不要求寫作法,但要保留作圖痕跡.
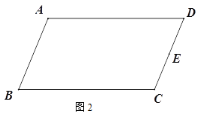
(1)如圖1,A為圓E上一點(diǎn),請用直尺(不帶刻度)和圓規(guī)作出圓內(nèi)接正方形;
(2)我們知道,三角形具有性質(zhì),三邊的垂直平分線相交于同一點(diǎn),三條角平分線相交于一點(diǎn),三條中線相交于一點(diǎn),事實上,三角形還具有性質(zhì):三條高交于同一點(diǎn),請運(yùn)用上述性質(zhì),只用直尺(不帶刻度)作圖:
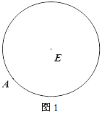
①如圖2,在□ABCD中,E為CD的中點(diǎn),作BC的中點(diǎn)F;
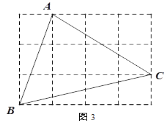
②圖3,在由小正方形組成的網(wǎng)格中,的頂點(diǎn)都在小正方形的頂點(diǎn)上,作△ABC的高AH
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com