【題目】計算題 1、化簡
2、若一次函數y=kx+b經過點A（3，4）、B（4，5），求這一次函數的解析式．
（1）先化簡，再求值： 
÷（2+ 
）
（2）若一次函數y=kx+b經過點A（3，4）、B（4，5），求這一次函數的解析式．
【答案】
（1）解： 
÷（2+ 
）
= 
= 
= 
；
（2）解：∵一次函數y=kx+b的圖象經過點A（3，4）和點B（4，5），
∴ 
，
解得： 
，
∴一次函數解析式為y=x+1
【解析】（1）先將括號里面通分，分子分母能分解因式的先分解因式，再把除法運算轉化為乘法運算，結果化成最簡分式。
（2）將A、B兩點坐標分別代入函數解析式，建立二元一次方程組，求解即可。
【考點精析】本題主要考查了分式的混合運算和確定一次函數的表達式的相關知識點，需要掌握運算的順序:第一級運算是加法和減法;第二級運算是乘法和除法;第三級運算是乘方.如果一個式子里含有幾級運算,那么先做第三級運算,再作第二級運算,最后再做第一級運算;如果有括號先做括號里面的運算.如順口溜:"先三后二再做一,有了括號先做里."當有多層括號時,先算括號內的運算,從里向外{[(?)]}；確定一個一次函數，需要確定一次函數定義式y=kx+b（k不等于0）中的常數k和b．解這類問題的一般方法是待定系數法才能正確解答此題．
科目：初中數學 來源： 題型：
【題目】如圖①、圖②，在給定的一張矩形紙片上作一個正方形，甲、乙兩人的作法如下：
甲：以點A為圓心，AD長為半徑畫弧，交AB于點E，以點D為圓心，AD長為半徑畫弧，交CD于點F，連接EF，則四邊形AEFD即為所求；
乙：作∠DAB的平分線，交CD于點M，同理作∠ADC的平分線，交AB于點N，連接MN，則四邊形ADMN即為所求．
對于以上兩種作法，可以做出的判定是( )
A.甲正確，乙錯誤B.甲、乙均正確
C.乙正確，甲錯誤D.甲、乙均錯誤
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】用兩種方法證明“四邊形的外角和等于360°”．
如圖，∠DAE、∠ABF、∠BCG、∠CDH是四邊形ABCD的四個外角．
求證：∠DAE＋∠ABF＋∠BCG＋∠CDH＝360°．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知△ABC中，AB=AC，點D，E分別在直線AB，AC上，且∠DEC=∠DCE
（1）如圖1，點D在線段AB上∠A=90°，若等腰直角三角形的邊與斜邊之比為
，求證：
（2）如圖2，若點D在線段AB的延長線上，∠A=60°，求證：EB=AD
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】利用完全平方公式因式分解在數學中的應用，請回答下列問題：
（1）因式分解：
_______．
（2）填空：
①當
時，代數式
_______．
②當
_______時，代數式
；
③代數式
的最小值是_______．
（3）拓展與應用：當
、
為何值時，代數式
有最小值，并求出這個最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲、 乙兩家超市以相同的價格出售同樣的商品．為了吸引顧客，各自推出不同的優惠方案： 在甲超市累計購買商品超出 300 元之后，超出部分按原價八折優惠；在乙超市累計購買商品超出 200 元之后，超出部分按原價九折優惠．設顧客預計累計購物 
元( 300)
（1）請用x 的代數式分別表示顧客在兩家超市購物所付的費用；
（2）試比較顧客到哪家超市購物更優惠？ 說明你的理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，從熱氣球C處測得地面A，B兩點的俯角分別是30°、45°，如果此時熱氣球C處的高度CD為100米，點A，D，B在同一直線上，則AB兩點的距離是（ ）
A.200米
B.200 
米
C.220 米
D.100（ 
）米
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了進一步了解七年級800名學生的身體素質情況，體育老師抽取七年級男女各25位學生進行一分鐘跳繩次數測試，以測試數據為樣本，繪制出部分頻數分布表和部分頻數分布直方圖．如下所示：
組別 | 次數x | 頻數（人數） |
第1組 | 80≤x＜100 | 6 |
第2組 | 100≤x＜120 | 8 |
第3組 | 120≤x＜140 |
|
第4組 | 140≤x＜160 | 16 |
第5組 | 160≤x＜180 | 6 |
請結合圖表完成下列問題：
(1)表中的
，跳繩次數低于140次的有
人，則
(2)請把頻數分布直方圖補充完整；
（3）若七年級學生一分鐘跳繩次數（x）達標要求是：x≥120．請估算七年級學生達標人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知反比例函數 
的圖象經過點（ 
，8），直線y=﹣x+b經過該反比例函數圖象上的點Q（4，m）．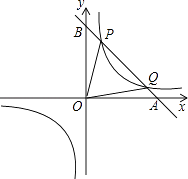
（1）求上述反比例函數和直線的函數表達式；
（2）設該直線與x軸、y軸分別相交于A、B兩點，與反比例函數圖象的另一個交點為P，連接0P、OQ，求△OPQ的面積．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
