
【題目】如圖所示,在平面直角坐標系中,O為坐標原點,直線y=kx+b經過點A(﹣2,﹣1),交y軸負半軸于點B,且∠ABO=30°,過點A作直線AC⊥x軸于點C,點P在直線AC上.

(1)k= ;b= ;
(2)設△ABP的面積為S,點P的縱坐標為m.
①當m>0時,求S與m之間的函數關系式;
②當S=2時,求m的值;
③當m>0且S=4時,以BP為邊作等邊△BPQ,請直接寫出符合條件的所有點Q的坐標.
【答案】(1)k=﹣![]() ;b=﹣1﹣2
;b=﹣1﹣2![]() ;(2)①S=1+m;②m的值為1或﹣3;③點Q的坐標為(﹣4﹣2
;(2)①S=1+m;②m的值為1或﹣3;③點Q的坐標為(﹣4﹣2![]() ,1﹣2
,1﹣2![]() )或(2+2
)或(2+2![]() ,1)
,1)
【解析】
(1)CD=![]() AC=
AC=![]() ,AD=2CD=
,AD=2CD=![]() ,則B(0,-1-2
,則B(0,-1-2![]() ),把點B和A(-2,-1)代入y=kx+b,即可求解;
),把點B和A(-2,-1)代入y=kx+b,即可求解;
(2)①當m>0,△ABP的面積為S=![]() (1+m)×2=1+m,即S=1+m;
(1+m)×2=1+m,即S=1+m;
②-1<m≤0時,△ABP的面積為S=![]() (1+m)×2=1+m,即S=1+m;當m<-1時,△ABP的面積為S=
(1+m)×2=1+m,即S=1+m;當m<-1時,△ABP的面積為S=![]() (-1-m)×2=-1-m,即S=-1-m;即可求解;
(-1-m)×2=-1-m,即S=-1-m;即可求解;
③以證明△BPQ是等邊三角形、△BQE≌△PBF(AAS),、△PQ'G≌△PBF(AAS),即可求解.
解:(1)設直線y=kx+b與x軸交于點D,如圖所示:

∵點A(﹣2,﹣1),
∴OC=2,AC=1,
∵AC⊥x軸,OB⊥x軸,
∴AC∥OB,
∴∠CAD=∠ABO=30°,
∴CD=![]() AC=
AC=![]() ,
,
∴AD=2CD=![]() ,
,
OD=CD+OC=![]() +2,
+2,
∴BD=2OD=![]() +4,OB=
+4,OB=![]() OD=1+2
OD=1+2![]() ,
,
∴B(0,﹣1﹣2![]() ),
),
把點B和A(﹣2,﹣1)代入y=kx+b得:并解得:
∴y=﹣![]() x﹣1﹣2
x﹣1﹣2![]() ,
,
故答案為:﹣![]() ;
;
(2)①當m>0,如圖1所示:
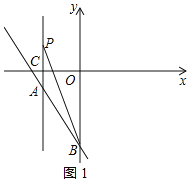
則PC=m,AP=AC+PC=1+m,
∴△ABP的面積為S=![]() (1+m)×2=1+m,即S=1+m;
(1+m)×2=1+m,即S=1+m;
②﹣1<m≤0時,如圖2所示:

則AP=1+m,
∴△ABP的面積為S=![]() (1+m)×2=1+m,即S=1+m;
(1+m)×2=1+m,即S=1+m;
當m<﹣1時,如圖3所示:

則AP=﹣1﹣m,
∴△ABP的面積為S=![]() (﹣1﹣m)×2=﹣1﹣m,即S=﹣1﹣m;
(﹣1﹣m)×2=﹣1﹣m,即S=﹣1﹣m;
把S=2代入S=1+m得:2=1+m,
解得:m=1;
把S=2代入S=﹣1﹣m得:2=﹣1﹣m,
解得:m=﹣3;
綜上所述,當S=2時,m的值為1或﹣3;
③以BP為邊作等邊△BPQ和等邊△BPQ',作QE⊥y軸于E,PF⊥y軸于F,如圖4所示:
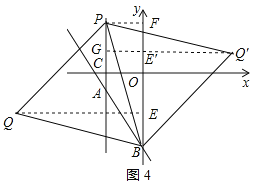
則PF=2,OF=3,BF=OF+OB=4+2![]() ,
,
當m>0且S=4時,4=1+m,
解得:m=3,
∴P(﹣2,3),
∴PC=3,AP=1+3=4,
∵AB=BD﹣AD=4,
∴AP=AB,
∴∠ABP=∠APB=![]() ∠CAD=15°,
∠CAD=15°,
∵AC∥OB,
∴∠PBF=∠APB=15°,
∵△BPQ是等邊三角形,
∴BQ=BP,∠PBQ=60°,
∴∠QBE=75°,∴∠BQE=90°﹣75°=15°=∠PBF,
在△BQE和△PBF中,
∠QEB=∠BFP=90°,∠BQE=∠PBF,BQ=PB,
∴△BQE≌△PBF(AAS),
∴QE=BF=4+2![]() ,BE=PF=2,
,BE=PF=2,
∴OE=OB﹣BE=2![]() ﹣1,
﹣1,
∴點Q的坐標為(﹣4﹣2![]() ,1﹣2
,1﹣2![]() );
);
作Q'G⊥PC于G,交y軸于E',
同理:△PQ'G≌△PBF(AAS),
∴Q'G=BF=4+2![]() ,PG=PF=2,
,PG=PF=2,
∴OE'=Q'G﹣OC=2+2![]() ,CG=PC﹣PG=1,
,CG=PC﹣PG=1,
∴點Q'的坐標為(2+2![]() ,1);
,1);
綜上所述,點Q的坐標為(﹣4﹣2![]() ,1﹣2
,1﹣2![]() )或(2+2
)或(2+2![]() ,1).
,1).


 周周清檢測系列答案
周周清檢測系列答案 輕巧奪冠周測月考直通高考系列答案
輕巧奪冠周測月考直通高考系列答案科目:初中數學 來源: 題型:
【題目】某建筑公司甲、乙兩個工程隊通過公開招標獲得某改造工程項目.已知甲隊單獨完成這項工程的時間是乙隊單獨完成這項工程時間的![]() 倍,由于乙隊還有其他任務,先由甲隊單獨做55天后,再由甲、乙兩隊合做20天,完成了該項改造工程任務.
倍,由于乙隊還有其他任務,先由甲隊單獨做55天后,再由甲、乙兩隊合做20天,完成了該項改造工程任務.
(Ⅰ)請根據題意求甲、乙兩隊單獨完成改造工程任務各需多少天;
(Ⅱ)這項改造工程共投資200萬元,如果按完成的工程量付款,那么甲、乙兩隊可獲工程款各多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,再添兩個條件不能夠全等的是( )

A.AB=A′B′,BC=B′C′B.AC=AC′,BC=BC′
C.∠A=∠A′,BC=B′C′D.∠A=∠A′,∠B=∠B′
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=-![]() x+b的圖象與x軸,y軸分別交于點A,B,與一次函數y=
x+b的圖象與x軸,y軸分別交于點A,B,與一次函數y=![]() x的圖象交于點M,點M的橫坐標為
x的圖象交于點M,點M的橫坐標為![]() ,在x軸上有一點P(a,0),過點P作x軸的垂線,分別交一次函數y=-
,在x軸上有一點P(a,0),過點P作x軸的垂線,分別交一次函數y=-![]() x+b和一次函數y=
x+b和一次函數y=![]() x的圖象于點C,D.
x的圖象于點C,D.

(1)點M的縱坐標是 ;b的值是 ;
(2)求線段AB的長;
(3)當CD=AB時,請直接寫出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年4月23日是 “世界讀書日”,宜賓市某中學舉行“多讀書,讀好書”活動,對學生的課外讀書時間進行了隨機問卷調查,用調查結果繪制了圖1、圖2兩幅統計圖(均不完整),請根據統計圖解答以下問題:
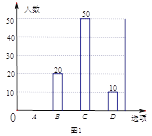
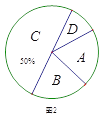
(1)本次接受問卷調查的學生共有________人,在扇形統計圖中“D”選項所占的百分比為________;
(2)扇形統計圖中,“B”選項所對應扇形圓心角為________度;
(3)請補全條形統計圖;
(4)若該校共有1200名學生,則該校學生課外讀書時間在“A”選項的約有_____人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在大課間活動中,同學們積極參加體育鍛煉,小龍在全校隨機抽取了一部分同學就“我最喜愛的體育項目”進行了一次調查(每位同學必選且只選一項).下面是他通過收集的數據繪制的兩幅不完整的統計圖,請你根據圖中提供的信息,解答以下問題:
(1)小龍一共抽取了 名學生.
(2)補全條形統計圖;
(3)求“其他”部分對應的扇形圓心角的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了改善小區環境,某小區決定要在一塊邊靠墻(墻長18m)的空地,修建一個矩形綠地ABCD,綠地一邊靠墻,另三邊用總長為40m的柵欄圍住(如圖),設AB邊為xm,綠地面積為ym2.
(1)求y與x之間的函數關系,并求出自變量x的取值范圍;
(2)綠地的面積能不能為200m2?如果能,求出x的值,如果不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小剛在實踐課上要做一個如圖1所示的折扇,折扇扇面的寬度AB是骨柄長OA的![]() ,折扇張開的角度為120°.小剛現要在如圖2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料長為24
,折扇張開的角度為120°.小剛現要在如圖2所示的矩形布料上剪下扇面,且扇面不能拼接,已知矩形布料長為24![]() cm,寬為21cm.小剛經過畫圖、計算,在矩形布料上裁剪下了最大的扇面,若不計裁剪和粘貼時的損耗,此時扇面的寬度AB為( )
cm,寬為21cm.小剛經過畫圖、計算,在矩形布料上裁剪下了最大的扇面,若不計裁剪和粘貼時的損耗,此時扇面的寬度AB為( )

A. 21cm B.20 cm C. 19cm D. 18cm
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com