
【題目】如圖,在△ABC中,∠A=90°,以AB為直徑的O交BC于D,點E為AC的中點,連接DE.
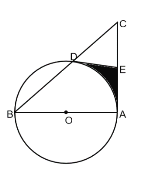
(1)求證:DE是O的切線;
(2)若∠BAD=50°,AC=6,CD=4,求圖中陰影部分的面積.
【答案】(1)詳見解析;(2)![]()
【解析】
(1)連接OD,DA,利用直角三角形的性質證明![]() ,利用等腰三角形的性質可得結論;
,利用等腰三角形的性質可得結論;
(2)證明△ADC∽△BAC,求解圓的半徑,利用S陰影=S四邊形OAED-S扇形AOD可得答案.
解:(1)連接OD,DA
∵AB是O的直徑,
∴∠BDA=∠CDA=90°
∵點E是AC的中點
∴在Rt△ACD中,DE=AE,
∴∠EDA=∠DAE
∵OD=OA
∴∠OAD=∠ODA
又∵∠BAC=90°
∴∠EDA+∠ODA=∠DAE+∠OAD=90°
即∠ODE=90°
∴OD⊥DE
又∵點D在O上
∴DE是O的切線·

(2)由題知∠ADC=∠BAC=90°,∠C=∠C
∴△ADC∽△BAC
∴![]() ,即
,即![]()
∴BC=9
在Rt△ABC中,由勾股定理可得AB=![]()
∴OA=![]() ,
,
連接![]()
![]()
![]() S四邊形OAED
S四邊形OAED![]()
∵OA=OD,DE=AE=3
∴S四邊形OAED ![]()
又∵弧BD所對圓周角為50°
∴∠BOD=100°,則∠AOD=80°
∴S扇形AOD 
∴S陰影=S四邊形OAED-S扇形AOD![]()



科目:初中數學 來源: 題型:
【題目】為宣傳普及新冠肺炎防治知識,引導學生做好防控.某校舉行了主題為“防控新冠,從我做起”的線上知識競賽活動,測試內容為20道判斷題,每道題5分,滿分100分.為了解八、九年級學生此次競賽成績的情況,分別隨機在八、九年級各抽取了20名參賽學生的成績.已知抽查得到的八年級的數據如下:
80,95,75,75,90,75,80,65,80,85,75,65,70,65,85,70,95,80,75,80.
為了便于分析數據,統計員對八年級數據進行了整理,得到了表一:
成績等級 | 分數(單位:分) | 學生數 |
|
| 5 |
|
|
|
|
|
|
|
| 2 |
八、九年級成績的平均數、中位數、優秀率如下:(分數80分以上、不含80分為優秀)
年級 | 平均數 | 中位數 | 優秀率 |
八年級 | 77.5 |
|
|
九年級 | 76 | 82.5 | 50% |
(1)根據題目信息填空:![]() ________,
________,![]() ________,
________,![]() ________;
________;
(2)八年級王宇和九年級程義的分數都為80分,請判斷王宇、程義在各自年級的排名哪位更靠前?請簡述你的理由;
(3)八年級被抽取的20名學生中,獲得![]() 等和
等和![]() 等的學生將被隨機選出2名,協助學校普及新冠肺炎防控知識,求這兩人都為
等的學生將被隨機選出2名,協助學校普及新冠肺炎防控知識,求這兩人都為![]() 等的概率.
等的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
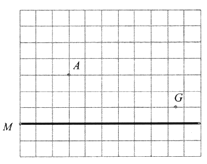
【題目】如圖,在每個小正方形的邊長為1的網格中,A,M,N均在格點上.在線段![]() 上有一動點B,以
上有一動點B,以![]() 為直角邊在
為直角邊在![]() 的右側作等腰直角
的右側作等腰直角![]() ,使
,使![]() ,
,![]() ,G是一個小正方形邊的中點.
,G是一個小正方形邊的中點.
(1)當點B的位置滿足![]() 時,求此時
時,求此時![]() 的長_______;
的長_______;
(2)請用無刻度的直尺,在如圖所示的網格中,畫出一個點C,使其滿足線段![]() 最短,并簡要說明點C的位置是如何找到的(不要求證明)____________.
最短,并簡要說明點C的位置是如何找到的(不要求證明)____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
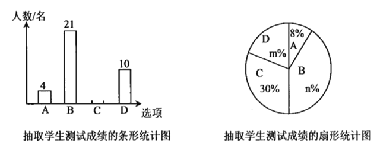
【題目】![]() 年
年![]() 月
月![]() 日,葫蘆島市九年級師生結束了兩個多月的線上教學和學習,正式回歸校園,在開學第一天,某校教導處老師為了解九年級學生對“新冠”傳播與防治知識的掌握情況,隨機抽取了部分學生進行了防疫知識的測試,測試后的成績,按得分劃分為
日,葫蘆島市九年級師生結束了兩個多月的線上教學和學習,正式回歸校園,在開學第一天,某校教導處老師為了解九年級學生對“新冠”傳播與防治知識的掌握情況,隨機抽取了部分學生進行了防疫知識的測試,測試后的成績,按得分劃分為![]() 四個等級,
四個等級,![]() :優秀,
:優秀,![]() :良好,
:良好,![]() :及格,
:及格,![]() :不及格,并繪制了如下不完整的條形統計圖和扇形統計圖.根據提供的信息,解答以下問題:
:不及格,并繪制了如下不完整的條形統計圖和扇形統計圖.根據提供的信息,解答以下問題:
(1)本次調查抽取的學生人數有多少人?
(2)扇形統計圖中![]() ,
,![]() 并補全條形統計圖;
并補全條形統計圖;
(3)已知該校九年級有![]() 名學生,學校決定對“不及格”的學生進行一次防疫知識的培訓,那么需要接受培訓的學生大約有多少人?
名學生,學校決定對“不及格”的學生進行一次防疫知識的培訓,那么需要接受培訓的學生大約有多少人?
(4)已知“優秀”的同學有![]() 名男生和
名男生和![]() 名女生,從中隨機抽取
名女生,從中隨機抽取![]() 名進行防疫知識的交流,請用畫樹狀圖或列表的方法,求恰好抽到一男一女的概率.
名進行防疫知識的交流,請用畫樹狀圖或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
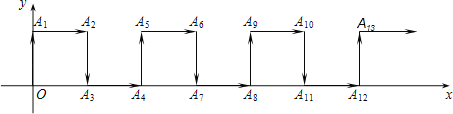
【題目】如圖,在平面直角坐標系中,一動點從原點O出發,按向上,向右,向下,向右的方向不斷地移動,每移動一個單位,得到點A1(0,1),A2(1,1),A3(1,0),A4(2,0),…那么點A2020的坐標為________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校園手機”現象越來越受到社會的關注.“五一”期間,小記者劉凱隨機調查了城區若干名學生和家長對中學生帶手機現象的看法,統計整理并制作了如圖所示的統計圖:
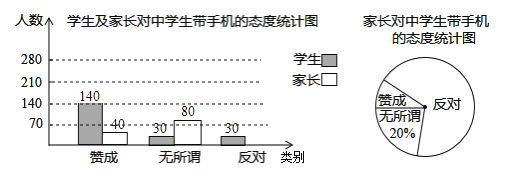
(1)求這次調查的家長人數,并補全圖①:
(2)求圖②中表示家長“贊成”的圓心角的度數;
(3)從這次接受調查的學生中,隨機抽查一個,恰好是“無所謂”態度的學生的概率是多少?
(4)為更深入的了解學生的看法,又從“贊成”的學生甲、乙、丙、丁四人中隨機選取2人,請用樹狀圖法或列表法求出恰好選中甲和乙的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
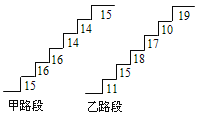
【題目】在某旅游景區上山的一條小路上,有一些斷斷續續的臺階,下圖是其中的甲、乙兩段臺階的示意圖,圖中的數字表示每一級臺階的高度(單位:cm).請你用所學過的有關統計知識,回答下列問題(數據:15,16,16,14,14,15的方差![]() ,數據:11,15,18,17,10,19的方差
,數據:11,15,18,17,10,19的方差![]() :
:
(1)分別求甲、乙兩段臺階的高度平均數;
(2)哪段臺階走起來更舒服?與哪個數據(平均數、中位數、方差和極差)有關?
(3)為方便游客行走,需要陳欣整修上山的小路,對于這兩段臺階路.在總高度及臺階數不變的情況下,請你提出合理的整修建議.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】桌面上有四張正面分別標有數字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它們除數字外其余全部相同,現將它們背面朝上洗勻.
的不透明卡片,它們除數字外其余全部相同,現將它們背面朝上洗勻.
(1)隨機翻開一張卡片,正面所標數字大于![]() 的概率為 ;
的概率為 ;
(2)隨機翻開一張卡片,從余下的三張卡片中再翻開一張,求翻開的兩張卡片正面所標數字之和是偶數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
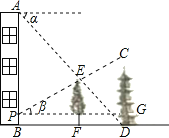
【題目】如圖,在一居民樓AB和塔CD之間有一棵樹EF,從樓頂A處經過樹頂E點恰好看到塔的底部D點,且俯角α為38°.從距離樓底B點2米的P處經過樹頂E點恰好看到塔的頂部C點,且仰角β為28°.已知樹高EF=8米,求塔CD的高度.(參考數據:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com