
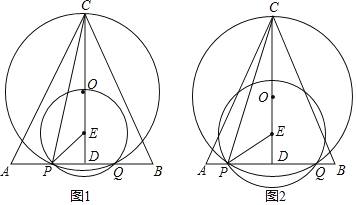
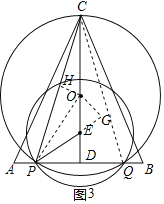
【題目】△ABC中,CA=CB,AB=![]() ,CD⊥AB于點D,CD=5,點O和點E在線段CD上,ED=1,點P在邊AB上,以E為圓心,EP為半徑的圓與AB邊的另一個交點為點Q(點P在點Q的左側),以O為圓心,OC為半徑的圓O恰好經過P、Q兩點,聯結CP,設線段AP的長度為x.
,CD⊥AB于點D,CD=5,點O和點E在線段CD上,ED=1,點P在邊AB上,以E為圓心,EP為半徑的圓與AB邊的另一個交點為點Q(點P在點Q的左側),以O為圓心,OC為半徑的圓O恰好經過P、Q兩點,聯結CP,設線段AP的長度為x.
(1)當圓E恰好經過點O時,求圓E的半徑;
(2)聯結CQ,設∠PCQ的正切值為y,求y與x的函數關系式及定義域;
(3)若∠PED=3∠PCE,求S△PCQ的值.
【答案】(1)![]() ﹣5;(2)y=
﹣5;(2)y=![]() (
(![]() <x<
<x<![]() );(3)
);(3)![]()
【解析】
(1)連接OP,設⊙E的半徑為r,根據OP2﹣OD2=PE2﹣DE2列出方程即可求出結論;
(2)連接OQ,根據等邊對等角可得∠OCQ=∠OQC,然后即可證出∠PCQ=∠DOQ,根據勾股定理即可推出m和x的關系,最后根據銳角三角函數即可求出y與x的函數關系式;
(3)連接CQ,OP,過點O作OH⊥CP于H,作CG⊥PE于G,根據相似三角形判定分別證出△EPO∽△ECP,△CHO∽△CDP,設OC=OP=m,根據相似三角形的性質列出比例式即可求出m的值,從而求出PQ和CD,即可求出結論.
解:(1)如圖1,連接OP,設⊙E的半徑為r,則PE=OE=r,OP=OC=4﹣r,OD=r+1,
∵CD⊥AB,
∴OP2﹣OD2=PE2﹣DE2,
即(4﹣r)2﹣(r+1)2=r2﹣12,
解得![]() (舍去),
(舍去),![]() ,
,
∴圓E的半徑r=![]() ﹣5.
﹣5.
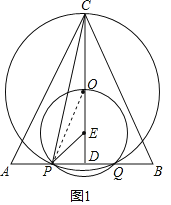
(2)如圖2,連接OQ,
∵OQ=OC,
∴∠OCQ=∠OQC
∵∠DOQ=∠OCQ+∠OQC
∴∠DOQ=2∠OCQ
∵∠PCD=∠QCD
∴∠PCQ=2∠QCD
∴∠PCQ=∠DOQ
設OC=OQ=m,則OD=5﹣m,
由勾股定理得DQ2=m2﹣(5﹣m)2=10m﹣25,
由題知:AP=x,
∴DQ=![]() ﹣x,
﹣x,
∴OD=5﹣m=![]() ﹣
﹣![]() ,
,
∴y=tan∠PCQ=tan∠DOQ=![]() =
=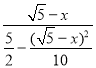 =
=![]()
∵![]()
∴![]() <x<
<x<![]() ,
,
∴y與x的函數關系式為 y=![]() (
(![]() <x<
<x<![]() ).
).
(3)如圖3,連接CQ,OP,過點O作OH⊥CP于H,作CG⊥PE于G,
∵OC=OP,
∴∠PCE=∠OPC,CH=![]() CP
CP
∵∠PED=3∠PCE,
∴∠OPE=∠OPC=∠PCE,
∴△EPO∽△ECP,OH=OG,
設OC=OP=m,
∵∠CHO=∠CDP=90°,
∴△CHO∽△CDP
∴![]() ,即
,即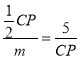
∴CP2=10m,CP=![]() ,PD2=10m﹣25,PE2=10m﹣24,
,PD2=10m﹣25,PE2=10m﹣24,
∵![]() ,
,
即![]()
∴![]() ,
,
解得:m1=0(舍去),![]() ,
,
∴PD=![]() =
=![]() ,PQ=2PD=
,PQ=2PD=![]()
∴![]() =
=![]() .
.



科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=﹣x2+bx+c交x軸負半軸于點A,交x軸正半軸于點B(4,0),交y軸正半軸于點C,OC=4OA,S△ABC=24.
(1)求拋物線的解析式;
(2)點P為第一象限拋物線上一點,過點P作PD⊥AB于點D,連接AP交y軸于點E,過點E作EG⊥PD于點G,設點P的橫坐標為t(t≤1),PG的長度為d,求d與t之間的函數關系式(不要求寫出自變量t的取值范圍);
(3)在(2)的條件下,過點B作BF⊥EG交EG的延長線于點F,點Q在線段GF上,連接DQ、PQ,將△DGQ沿DQ折疊后,點G的對稱點為點H,DH交BF于點M,連接MQ并延長交DP的延長線于點N,當∠DQM=45°,tan∠PQN=![]() 時,求直線PQ的解析式.
時,求直線PQ的解析式.

查看答案和解析>>
科目:初中數學 來源: 題型:
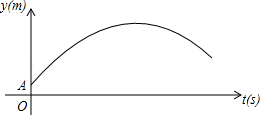
【題目】如圖,某足球運動員站在點O處練習射門.將足球從離地面0.5m的A處正對球門踢出(點A在y軸上),足球的飛行高度y(單位:m)與飛行時間t(單位:s)之間滿足函數關系y=at2+5t+c,己知足球飛行0.8s時,離地面的高度為3.5m.
(1)a= ,c= ;
(2)當足球飛行的時間為多少時,足球離地面最高?最大高度是多少?
(3)若足球飛行的水平距離x(單位:m)與飛行時間t(單位:s)之間具有函數關系x=10t,已知球門的高度為2.44m,如果該運動員正對球門射門時,離球門的水平距離為28m,他能否將球直接射入球門?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系 xOy 中,已知拋物線y= x2 -2px+q.
(1)當p=2 時,
①拋物線的頂點坐標橫坐標為____ ___,縱坐標為__________(用含 q 的式子表示);
②若點 A(-1,y1),B(x2,y2 )都在拋物線上,且y2 >y1,令x2 = m,則 m的取值范圍是_____________;
(2)已知點 M(3,2),將點 M 向左平移 5 個單位長度,得到點 N.當q=6 時,若拋物線與線段 MN 恰有一個公共點,結合函數圖象,求 p 的取值范圍為_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司銷售一種進價為20元/個的計算器,其銷售量y(萬個)與銷售價格x(元/個)的變化如下表:
價格x(元/個) | … | 30 | 40 | 50 | 60 | … |
銷售量y(萬個) | … | 5 | 4 | 3 | 2 | … |
同時,銷售過程中的其他開支(不含進價)總計40萬元.
(1)觀察并分析表中的y與x之間的對應關系,用所學過的一次函數,反比例函數或二次函數的有關知識寫出y(萬個)與x(元/個)的函數解析式.
(2)求出該公司銷售這種計算器的凈得利潤z(萬元)與銷售價格x(元/個)的函數解析式,銷售價格定為多少元時凈得利潤最大,最大值是多少?
(3)該公司要求凈得利潤不能低于40萬元,請寫出銷售價格x(元/個)的取值范圍,若還需考慮銷售量盡可能大,銷售價格應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
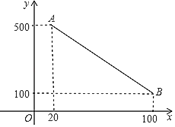
【題目】小明家買了一臺充電式自動掃地機,每次完成充電后,在使用時掃地機會自動根據設定掃地時間,來確定掃地的速度(以使每次掃地結束時盡量把所儲存的電量用完),如圖是“設定掃地時間”與“掃地速度”之間的函數圖象(線段AB),其中設定掃地時間為x分鐘,掃地速度為y平方分米/分鐘.
(1)求y關于x的函數解析式;
(2)現在小明需要掃地機完成180平方米的掃地任務,他應該設定的掃地時間為多少分鐘?
查看答案和解析>>
科目:初中數學 來源: 題型:
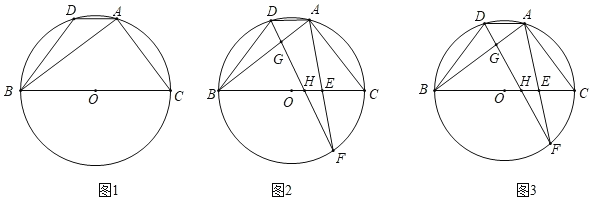
【題目】已知:△ABC內接于⊙O,點D為弧AB上一點,連接AD,BD,且AC=BD.
(1)如圖1,求證:AD∥BC;
(2)如圖2,點E為BC上一點,連接AE并延長交⊙O于點F,連接DF分別交AB,BC于點G,H,∠BAD+∠CAF=∠BGH,求證:AD=AG;
(3)如圖3,在(2)的條件下,當∠BAF=60°,AE=EF,BH=6時,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
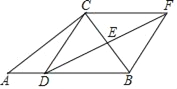
【題目】如圖,在△ABC中,D是AB邊上任意一點,E是BC邊中點,過點C作AB的平行線,交DE的延長線于點F,連接BF,CD.
(1)求證:四邊形CDBF是平行四邊形;
(2)若∠FDB=30°,∠ABC=45°,BC=4![]() ,求DF的長.
,求DF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com