Question

【題目】如圖，在△ABC中，∠C＝90°，∠B＝30°，以A為圓心，任意長為半徑畫弧分別交AB、AC于點M和N，再分別以M、N為圓心，大于MN的長為半徑畫弧，兩弧交于點P，連接AP，并廷長交BC于點D，則下列說法中正確的個數是（　　）

①AD是∠BAC的平分線

②∠ADC＝60°

③點D在AB的垂直平分線上

④若AD＝2dm，則點D到AB的距離是1dm

⑤S△DAC：S△DAB＝1：2

A.2B.3C.4D.5

Answer 1

【答案】D

【解析】

①根據作圖的過程可以判定AD是∠BAC的角平分線；
②利用角平分線的定義可以推知∠CAD=30°，則由直角三角形的性質來求∠ADC的度數；
③利用等角對等邊可以證得△ADB的等腰三角形，由等腰三角形的“三線合一”的性質可以證明點D在AB的中垂線上；
④作DH⊥AB于H，由∠1=∠2，DC⊥AC，DH⊥AB，推出DC=DH即可解決問題；
⑤利用30度角所對的直角邊是斜邊的一半、三角形的面積計算公式來求兩個三角形的面積之比．

解：①根據作圖的過程可知，AD是∠BAC的平分線，故①正確；

②如圖，∵在△ABC中，∠C＝90°，∠B＝30°，

∴∠CAB＝60°．

又∵AD是∠BAC的平分線，

∴∠1＝∠2＝∠CAB＝30°，

∴∠3＝90°﹣∠2＝60°，即∠ADC＝60°．故②正確；

③∵∠1＝∠B＝30°，

∴AD＝BD，

∴點D在AB的中垂線上．故③正確；

④作DH⊥AB于H，

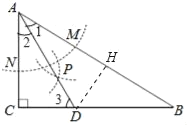
∵∠1＝∠2，DC⊥AC，DH⊥AB，

∴DC＝DH，

在Rt△ACD中，CD＝AD＝1dm，

∴點D到AB的距離是1dm；故④正確，

⑤在Rt△ACB中，∵∠B＝30°，

∴AB＝2AC，

∴S△DAC：S△DAB＝ACCD：ABDH＝1：2；故⑤正確．

綜上所述，正確的結論是：①②③④⑤，共有5個．

故選：D．