
【題目】如圖,BD是△ABC的角平分線,它的垂直平分線分別交AB,BD,BC于點E,F,G,連接ED,DG.
(1)△EFD≌△GFB.
(2)試判斷四邊形FBGD的形狀,并說明理由.
(3)當△ABC滿足條件時,四邊形FBGD是正方形(不用說明理由).
【答案】
(1)解:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
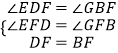 ,
,
∴△EFD≌△GFB
(2)解:四邊形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
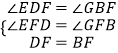 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四邊形EBGD是菱形
(3)∠ABC=90°
【解析】解:(3)當△ABC是直角三角形,即∠ABC=90°時,四邊形FBGD是正方形,根據有一個角是直角的菱形是正方形可以得出.
所以答案是:∠ABC=90°.
【考點精析】利用菱形的性質和正方形的判定方法對題目進行判斷即可得到答案,需要熟知菱形的四條邊都相等;菱形的對角線互相垂直,并且每一條對角線平分一組對角;菱形被兩條對角線分成四個全等的直角三角形;菱形的面積等于兩條對角線長的積的一半;先判定一個四邊形是矩形,再判定出有一組鄰邊相等;先判定一個四邊形是菱形,再判定出有一個角是直角.


 課時訓練江蘇人民出版社系列答案
課時訓練江蘇人民出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線m與直線n相交于點O,A、B兩點同時從點O出發,點A以每秒x個單位長度沿直線n向左運動,點B以每秒y個單位長度沿直線m向上運動。
(1)若運動1s時,點B比點A多運動1個單位;運動2s時,點B與點A運動的路程和為6個單位,則x=_________,y=___________.
(2)如圖,當直線m與直線n垂直時,設∠BAO和∠ABO的角平分線相交于點P.在點A、B在運動的過程中,∠APB的大小是否會發生變化?若不發生變化,請求出其值(寫出主要過程);若發生變化,請說明理由.
(3)如圖,將(2)中的直線n不動,直線m繞點O按順時針方向旋轉α(0<ɑ<90),其他條件不變.ⅰ)用含有α的式子表示∠APB的度數____________.
ⅱ)如果再分別作△ABO的兩個外角∠BAC,∠ABD的角平分線相交于點Q,并延長BP、QA交于點M.則下列結論正確的是___________(填序號) .
①APB與∠Q互補;②∠Q與∠M互余;③∠APB-∠M為定值;④∠M-∠Q為定值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程組解應用題:
為了保護環境,深圳某公交公司決定購買一批共10臺全新的混合動力公交車,現有A、B兩種型號,其中每臺的價格,年省油量如下表:
A | B | |
價格(萬元/臺) | a | b |
節省的油量(萬升/年) | 2.4 | 2 |
經調查,購買一臺A型車比購買一臺B型車多20萬元,購買2臺A型車比購買3臺B型車少60萬元.
(1)請求出a和b;
(2)若購買這批混合動力公交車每年能節省22.4萬汽油,求購買這批混合動力公交車需要多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,輪船沿正南方向以33海里/時的速度勻速航行,在m處觀測到燈塔p在西偏南69°方向下,航行2小時后到達n處,觀測燈塔p在西偏南57°方向上,若該船繼續向南航行至離燈塔最近位置,求此時輪船離燈塔的距離約為多少海里?(結果精確到整數,參考數據:tan33°≈ ![]() ,sin33°≈
,sin33°≈ ![]() ,cos33°≈
,cos33°≈ ![]() ,tan21°≈
,tan21°≈ ![]() ,sin21°≈
,sin21°≈ ![]() ,c0s21°≈
,c0s21°≈ ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,點E是邊CD上一點,且BC=EC,CF⊥BE交AB于點F,P是EB延長線上一點,下列結論:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC,其中正確結論的個數為( )
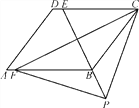
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,把直角三角形![]() 的直角頂點
的直角頂點![]() 放在直線
放在直線![]() 上,射線
上,射線![]() 平分
平分![]() .
.
(1)如圖,若![]() ,求
,求![]() 的度數.
的度數.
(2)若![]() ,則
,則![]() 的度數為 .
的度數為 .
(3)由(1)和(2),我們發現![]() 和
和![]() 之間有什么樣的數量關系?
之間有什么樣的數量關系?
(4)若將三角形![]() 繞點
繞點![]() 旋轉到如圖所示的位置,試問
旋轉到如圖所示的位置,試問![]() 和
和![]() 之間的數量關系是否發生變化?請說明理由.
之間的數量關系是否發生變化?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著幾何部分的學習,小鵬對幾何產生了濃厚的興趣,他最喜歡利用手中的工具畫圖了![]() 如圖,作一個
如圖,作一個![]() ,以O為圓心任意長為半徑畫弧分別交OA,OB于點C和點D,將一副三角板如圖所示擺放,兩個直角三角板的直角頂點分別落在點C和點D,直角邊中分別有一邊與角的兩邊重合,另兩條直角邊相交于點P,連接
,以O為圓心任意長為半徑畫弧分別交OA,OB于點C和點D,將一副三角板如圖所示擺放,兩個直角三角板的直角頂點分別落在點C和點D,直角邊中分別有一邊與角的兩邊重合,另兩條直角邊相交于點P,連接![]() 小鵬通過觀察和推理,得出結論:OP平分
小鵬通過觀察和推理,得出結論:OP平分![]() .
.
你同意小鵬的觀點嗎?如果你同意小鵬的觀點,試結合題意寫出已知和求證,并證明.
已知:![]() 中,______
中,______![]() ______,______
______,______![]() ______,______
______,______![]() ______.
______.
求證:OP平分![]() .
.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,點A,B,C滿足二次函數y=ax2+bx的表達式,則對該二次函數的系數a和b判斷正確的是( )
A.a>0,b>0
B.a<0,b<0
C.a>0,b<0
D.a<0,b>0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com