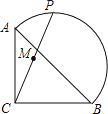
【題目】如圖，在等腰RtABC中，
，點P在以斜邊AB為直徑的半圓上，M為PC的中點.當點P沿半圓從點A運動至點B時，點M運動的路徑長是（ ）
A. 
B. 2
C. 
D. 4
【答案】B
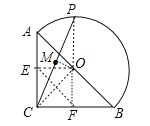
【解析】分析：取AB的中點O、AC的中點E、BC的中點F，連結OC、OP、OM、OE、OF、EF，如圖，利用等腰直角三角形的性質得到AB=
BC=8，則OC=
AB=4，OP=AB=4，再根據等腰三角形的性質得OM⊥PC，則∠CMO=90°，于是根據圓周角定理得到點M在以OC為直徑的圓上，由于點P點在A點時，M點在E點；點P點在B點時，M點在F點，則利用四邊形CEOF為正方得到EF=OC=4，所以M點的路徑為以EF為直徑的半圓，然后根據圓的周長公式計算點M運動的路徑長．
詳解：取AB的中點O、AC的中點E、BC的中點F，連結OC、OP、OM、OE、OF、EF，如圖，∵在等腰Rt△ABC中，AC=BC=4，∴AB=BC=8，∴OC=AB=4，OP=AB=4．
∵M為PC的中點，∴OM⊥PC，∴∠CMO=90°，∴點M在以OC為直徑的圓上，點P點在A點時，M點在E點；點P點在B點時，M點在F點，易得四邊形CEOF為正方形，EF=OC=4，∴M點運動的路徑為以EF為直徑的半圓，∴點M運動的路徑長=4π=2π． 故選B．
新課標同步訓練系列答案
一線名師口算應用題天天練一本全系列答案科目：初中數學 來源： 題型：
【題目】如圖，在四邊形ABCD中，AD∥BC，DE⊥BC，垂足為點E，連接AC交DE于點F，點G為AF的中點，∠ACD=2∠ACB．若DG=3，EC=1，則DE的長為（ ）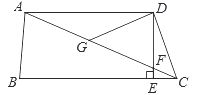
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明元旦節吃完晚飯后6點過還沒到7點，他陪他媽到成華區SM廣場去買東西，離家時他發現他家的時鐘上時針與分針剛好重合，他離家的時間是_______(用幾點幾分幾秒表示，注意“四舍五入”).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：菱形ABCD中，∠B＝60°，將含60°角的直角三角板的60°角的頂點放到菱形ABCD的頂點A處，兩邊分別與菱形的邊BC，CD交于點F，E.
(1)(如圖1)求證：AE=AF；
(2)連結EF，交AC于點H(如圖2)，試探究AB，AF，AH之間的關系；
(3)若AB＝6，EF＝2
，且CE＜DE，求FH的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點O是邊長為
的等邊△ABC的內心，將△OBC繞點O逆時針旋轉30°得到△OB1C1，B1C1交BC于點D，B1C1交AC于點E，則CE=( )
A. 2 B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
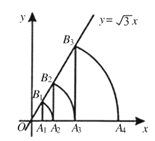
【題目】如圖，已知直線y＝
x，點A1的坐標為(1，0)，過點A1作x軸的垂線交直線于點B1，以原點O為圓心，OB1的長為半徑畫弧交x軸于點A2；再過點A2作x軸的垂線交直線于點B2，以原點O為圓心，OB2的長為半徑畫弧交x軸于點A3，…，按此做法進行下去，則點A6的坐標為____________．
查看答案和解析>>
科目：初中數學 來源： 題型：
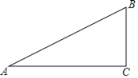
【題目】如圖，Rt△ABC中，∠C=90°，∠A=30°．
（1）作線段AB的垂直平分線DE，垂足為點E，交AC于點D，要求用尺規作圖，保留作圖痕跡，標注有關字母，不要求寫作法和證明；
（2）連接BD，直接寫出∠CBD的度數；
（3）如果△BCD的面積為4，請求出△BAD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如果關于x的一元二次方程ax2+bx+c=0有兩個實根，且其中一個根為另一根的2倍，則稱這樣的方程為“倍根方”，以下關于倍根方程的說法正確的是______（填正確序號）
①方程x2﹣x﹣2=0是倍根方程．
②若（x﹣2）（mx+n）=0是倍根方程，則4m2+5mn+n2=0．
③若點（p，q）在反比例函數y=
的圖象上，則關于x的方程px2+3x+q=0是倍根方程．
④若方程ax2+bx+c=0是倍根方程且相異兩點M（1+t，s）、N（4﹣t，s）都在拋物線y=ax2+bx+c上，則方程ax2+bx+c=0必有一個根為
．
查看答案和解析>>
科目：初中數學 來源： 題型：
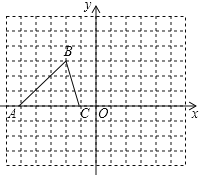
【題目】已知△ABC的三個頂點的坐標分別為A（﹣5，0）、B（﹣2，3）、C（﹣1，0）
（1）畫出△ABC關于坐標原點O成中心對稱的△
；
（2）將△ABC繞坐標原點O順時針旋轉90°，畫出對應的△
，
（3）若以
、
、
、
為頂點的四邊形為平行四邊形，請直接寫出在第四象限中的坐標____．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com