
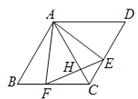
【題目】已知:菱形ABCD中,∠B=60°,將含60°角的直角三角板的60°角的頂點放到菱形ABCD的頂點A處,兩邊分別與菱形的邊BC,CD交于點F,E.
(1)(如圖1)求證:AE=AF;
(2)連結EF,交AC于點H(如圖2),試探究AB,AF,AH之間的關系;
(3)若AB=6,EF=2![]() ,且CE<DE,求FH的長.
,且CE<DE,求FH的長.


【答案】(1)見解析;(2)見解析;(3)![]()
【解析】分析:(1)由菱形的性質得到AD=AC, ∠ACB=∠D,從而用ASA判定出△ACF≌△ADE.
(2)由AE=AF,∠EAF=600,得到△AEF是等邊三角形,進而得到∠BAF=∠CAE,從而有△BAF∽△CAH,由相似三角形的性質即可得到結論.
(3)由等邊三角形的性質得到AF=EF=AE,再由AF2=AB·AH,得到AH的長,進而得到CH的長,通過證明△CEH∽△DAE,得到![]() ,進而求出CE、EH,FH的長.
,進而求出CE、EH,FH的長.
詳解:(1)連結AC.

∵ABCD是菱形,∠B=60°,
∴∠BAD=∠BCD=120°,∠D=60°,
∠ACD=∠ACB=![]() ∠BCD,∠BAC=∠DAC=
∠BCD,∠BAC=∠DAC=![]() ∠BAD.
∠BAD.
∴∠ACB=∠DAC=∠D=60°.
∴AD=AC.
∵∠EAF=60°,∴∠CAF+∠CAE=∠DAE+∠CAE.
∴∠CAF=∠DAE.
∴△ACF≌△ADE.
∴AE=AF.
(2)∵AE=AF,∠EAF=600,∴△AEF是等邊三角形.
∴∠AEF=600=∠B.
∴∠BAF+∠CAF=∠CAE+∠CAF=600.
∴∠BAF=∠CAE.
∴△BAF∽△CAH.
∴![]() .∴AB·AH=AE·AF,即AF2=AB·AH.
.∴AB·AH=AE·AF,即AF2=AB·AH.
(3)∵△AEF是等邊三角形,∴AF=EF=AE.
∵AF2=AB·AH,AB=6,EF=2![]() ,∴AH=
,∴AH=![]() .
.
∵∠B=∠ACB=600,∴AB=AC=6.
∴CH=AC-AH=6-![]() =
=![]() .
.
∵∠AEF=600,∴∠CEH+∠AED=1200.
∵∠D=600,∴∠DAE+∠AED=1200.
∴∠CEH=∠DAE.
∵∠ACD=∠D=600,∴△CEH∽△DAE.
∴![]() .
.
∵四邊形ABCD是菱形,∴AB=BC=CD=AD=6,
∴![]() .∴CE=2或CE=4.
.∴CE=2或CE=4.
∵CE<DE,∴CE=2.
∴![]() .∴EH=
.∴EH=![]() .∴FH=EF-EH=
.∴FH=EF-EH=![]() .
.


 手拉手全優練考卷系列答案
手拉手全優練考卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,正方形OABC的邊長為4,對角線相交于點P,頂點A、C分別在x軸、y軸的正半軸上,拋物線L經過0、P、A三點,點E是正方形內的拋物線上的動點.
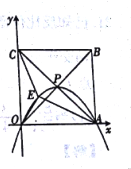
(1)點P的坐標為______
(2)求拋物線L的解析式.
(3)求△OAE與△OCE的面積之和的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】仔細填一填:
把下列各數填入相應的大括號里:
5,-1,0,-6,+8,0.3,-![]() ,+
,+![]() ,-0.72,…
,-0.72,…
① 正數集合:{ __________________ …}
② 整數集合:{__________________…}
③ 負數集合:{ __________________ …}
④ 分數集合:{__________________ …}
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】通過學習絕對值,我們知道![]() 的幾何意義是數軸上表示數
的幾何意義是數軸上表示數![]() 在數軸上的對應點與原點的距離,如:
在數軸上的對應點與原點的距離,如:![]() 表示
表示![]() 在數軸上的對應點到原點的距離.
在數軸上的對應點到原點的距離.![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在數軸上對應的兩點之間的距離,類似的,
在數軸上對應的兩點之間的距離,類似的,![]() ,即
,即![]() 表示
表示![]() 、
、![]() 在數軸上對應的兩點之間的距離;一般地,點
在數軸上對應的兩點之間的距離;一般地,點![]() ,
,![]() 在數軸上分別表示數
在數軸上分別表示數![]() 、
、![]() ,那么
,那么![]() ,
,![]() 之間的距離可表示為
之間的距離可表示為![]() .
.
請根據絕對值的幾何意義并結合數軸解答下列問題:
(1)數軸上表示![]() 和
和![]() 的兩點之間的距離是___;數軸上
的兩點之間的距離是___;數軸上![]() 、
、![]() 兩點的距離為
兩點的距離為![]() ,點
,點![]() 表示的數是
表示的數是![]() ,則點
,則點![]() 表示的數是___.
表示的數是___.
(2)點![]() ,
,![]() ,
,![]() 在數軸上分別表示數
在數軸上分別表示數![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到點
到點![]() .點
.點![]() 的距離之和可表示為_ (用含絕對值的式子表示);若
的距離之和可表示為_ (用含絕對值的式子表示);若![]() 到點
到點![]() .點
.點![]() 的距離之和有最小值,則
的距離之和有最小值,則![]() 的取值范圍是_ __.
的取值范圍是_ __.
(3)![]() 的最小值為_ __.
的最小值為_ __.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,①任意有理數![]() 的倒數是
的倒數是![]() ,②相反數等于自身的數只有一個,③海拔-155米表示海平面下155米,④絕對值大于本身的數一定是負數,⑤零是最小的自然數,⑥有理數包含正有理數和負有理數,⑦任意有理數
,②相反數等于自身的數只有一個,③海拔-155米表示海平面下155米,④絕對值大于本身的數一定是負數,⑤零是最小的自然數,⑥有理數包含正有理數和負有理數,⑦任意有理數![]() 的相反數是
的相反數是![]() .正確的有( )個
.正確的有( )個
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】夏師傅是一名徒步運動的愛好者,他用手機軟件記錄了某個月(30天)每天徒步的步數(單位:萬步),將記錄結果繪制成了如圖所示的統計圖.在這組徒步數據中,眾數和中位數分別是( )

A. 1.2,1.3 B. 1.4,1.3 C. 1.4,1.35 D. 1.3,1.3
查看答案和解析>>
科目:初中數學 來源: 題型:
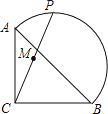
【題目】如圖,在等腰RtABC中,![]() ,點P在以斜邊AB為直徑的半圓上,M為PC的中點.當點P沿半圓從點A運動至點B時,點M運動的路徑長是( )
,點P在以斜邊AB為直徑的半圓上,M為PC的中點.當點P沿半圓從點A運動至點B時,點M運動的路徑長是( )
A. ![]() B. 2
B. 2![]() C.
C. ![]() D. 4
D. 4![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把一個直角三角形ACB(∠ACB=90°)繞著頂點B順時針旋轉60°,使得點C旋轉到AB邊上的一點D,點A旋轉到點E的位置.F,G分別是BD,BE上的點,BF=BG,延長CF與DG交于點H.

(1)求證:CF=DG;
(2)求出∠FHG的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
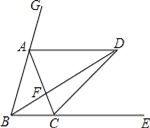
【題目】如圖,已知點A、C分別在∠GBE的邊BG、BE上,且AB=AC,AD∥BE,∠GBE的平分線與AD交于點D,連接CD.
求證:①AB=AD;
②CD平分∠ACE.
【答案】詳見解析.
【解析】(1)∵AD∥BE,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABD=∠ADB,
∴AB=AD;
(2)∵AD∥BE,
∴∠ADC=∠DCE,
由①知AB=AD,
又∵AB=AC,
∴AC=AD,
∴∠ACD=∠ADC,
∴∠ACD=∠DCE,
∴CD平分∠ACE;
點睛:角平分線問題的輔助線添加及其解題模型.
①垂兩邊:如圖(1),已知![]() 平分
平分![]() ,過點
,過點![]() 作
作![]() ,
, ![]() ,則
,則![]() .
.
②截兩邊:如圖(2),已知![]() 平分
平分![]() ,點
,點![]()
![]() 上,在
上,在![]() 上截取
上截取![]() ,則
,則![]() ≌
≌![]() .
.
③角平分線+平行線→等腰三角形:
如圖(3),已知![]() 平分
平分![]() ,
, ![]() ,則
,則![]() ;
;
如圖(4),已知![]() 平分
平分![]()
![]() ,則
,則![]() .
.
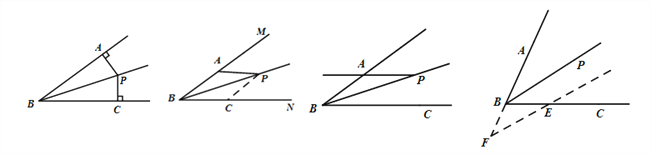
(1) (2) (3) (4)
④三線合一(利用角平分線+垂線→等腰三角形):
如圖(5),已知![]() 平分
平分![]() ,且
,且![]() ,則
,則![]() ,
, ![]() .
.
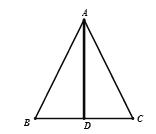
(5)
【題型】解答題
【結束】
26
【題目】如圖①,AB為半圓的直徑,O為圓心,C為圓弧上一點,AD垂直于過C點的切線,垂足為D,AB的延長線交直線CD于點E.
(1)求證:AC平分∠DAB;
(2)若AB=4,B為OE的中點,CF⊥AB,垂足為點F,求CF的長;
(3)如圖②,連接OD交AC于點G,若![]() ,求sinE的值.
,求sinE的值.
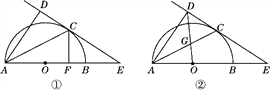
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com