【題目】如果關(guān)于x的一元二次方程ax2+bx+c=0有兩個(gè)實(shí)根，且其中一個(gè)根為另一根的2倍，則稱(chēng)這樣的方程為“倍根方”，以下關(guān)于倍根方程的說(shuō)法正確的是______（填正確序號(hào)）
①方程x2﹣x﹣2=0是倍根方程．
②若（x﹣2）（mx+n）=0是倍根方程，則4m2+5mn+n2=0．
③若點(diǎn)（p，q）在反比例函數(shù)y=
的圖象上，則關(guān)于x的方程px2+3x+q=0是倍根方程．
④若方程ax2+bx+c=0是倍根方程且相異兩點(diǎn)M（1+t，s）、N（4﹣t，s）都在拋物線(xiàn)y=ax2+bx+c上，則方程ax2+bx+c=0必有一個(gè)根為
．
【答案】②③④．
【解析】試題解析：①解方程
得： 
∴方程
不是倍根方程，故①錯(cuò)誤；
②
是倍根方程，且
∴
或
故②正確；
③∵點(diǎn)
在反比例函數(shù)
的圖象上，
解方程
得： 
故③正確；
④∵方程
是倍根方程，
∴設(shè)
∵相異兩點(diǎn)
都在拋物線(xiàn)
上，
∴拋物線(xiàn)的對(duì)稱(chēng)軸
故④正確．
故答案為：②③④．
名校課堂系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】仔細(xì)填一填：
把下列各數(shù)填入相應(yīng)的大括號(hào)里：
5，－1，0，－6，＋8，0.3，－
，＋
，－0.72，…
① 正數(shù)集合：{ __________________ …}
② 整數(shù)集合：{__________________…}
③ 負(fù)數(shù)集合：{ __________________ …}
④ 分?jǐn)?shù)集合：{__________________ …}
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，在等腰RtABC中，
，點(diǎn)P在以斜邊AB為直徑的半圓上，M為PC的中點(diǎn).當(dāng)點(diǎn)P沿半圓從點(diǎn)A運(yùn)動(dòng)至點(diǎn)B時(shí)，點(diǎn)M運(yùn)動(dòng)的路徑長(zhǎng)是（ ）
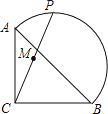
A. 
B. 2
C. 
D. 4
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，把一個(gè)直角三角形ACB（∠ACB=90°）繞著頂點(diǎn)B順時(shí)針旋轉(zhuǎn)60°，使得點(diǎn)C旋轉(zhuǎn)到AB邊上的一點(diǎn)D，點(diǎn)A旋轉(zhuǎn)到點(diǎn)E的位置．F，G分別是BD，BE上的點(diǎn)，BF=BG，延長(zhǎng)CF與DG交于點(diǎn)H．
（1）求證：CF=DG；
（2）求出∠FHG的度數(shù)．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
【題目】如圖，已知：∠BAC的平分線(xiàn)與BC的垂直平分線(xiàn)DG相交于點(diǎn)D，DE⊥AB，DF⊥AC，垂足分別為E、F，AB=6，AC=3，則BE=_____．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
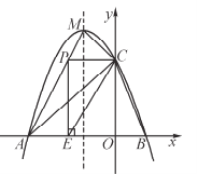
【題目】如圖，拋物線(xiàn)
與
軸交于A、B兩點(diǎn)，與y軸交于點(diǎn)C（0，3），且此拋物線(xiàn)的頂點(diǎn)坐標(biāo)為M（-1，4）.
（1）求此拋物線(xiàn)的解析式；
（2）設(shè)點(diǎn)D為已知拋物線(xiàn)對(duì)稱(chēng)軸上的任意一點(diǎn)，當(dāng)△ACD面積等于6時(shí)，求點(diǎn)D的坐標(biāo)；
（3）點(diǎn)P在線(xiàn)段AM上，當(dāng)PC與y軸垂直時(shí)，過(guò)點(diǎn)P作軸的垂線(xiàn)，垂足為E，將△PCE沿直線(xiàn)CB翻折，使點(diǎn)P的對(duì)應(yīng)點(diǎn)P'與P、E、C處在同一平面內(nèi)，請(qǐng)求出P'坐標(biāo)，并判斷點(diǎn)P'是否在拋物線(xiàn)上.
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
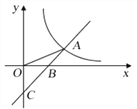
【題目】如圖，直線(xiàn)
與
軸交于點(diǎn)C，與
軸交于點(diǎn)B，與反比例函數(shù)
的圖象在第一象限交于點(diǎn)A，連接OA，且
．
（1）求ΔBOC的面積．
（2）求點(diǎn)A的坐標(biāo)和反比例函數(shù)的解析式．
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
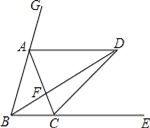
【題目】如圖，已知點(diǎn)A、C分別在∠GBE的邊BG、BE上，且AB=AC，AD∥BE，∠GBE的平分線(xiàn)與AD交于點(diǎn)D，連接CD．
求證：①AB=AD；
②CD平分∠ACE．
【答案】詳見(jiàn)解析.
【解析】(1)∵AD∥BE，
∴∠ADB=∠DBC，
∵BD平分∠ABC，
∴∠ABD=∠DBC，
∴∠ABD=∠ADB，
∴AB=AD；
（2）∵AD∥BE，
∴∠ADC=∠DCE，
由①知AB=AD，
又∵AB=AC，
∴AC=AD，
∴∠ACD=∠ADC，
∴∠ACD=∠DCE，
∴CD平分∠ACE；
點(diǎn)睛：角平分線(xiàn)問(wèn)題的輔助線(xiàn)添加及其解題模型.
①垂兩邊：如圖（1），已知
平分
，過(guò)點(diǎn)
作
， 
，則
.
②截兩邊：如圖（2），已知
平分
，點(diǎn)
上，在
上截取
，則
≌
.
③角平分線(xiàn)+平行線(xiàn)→等腰三角形：
如圖（3），已知
平分
， 
，則
；
如圖（4），已知
平分
，則
.
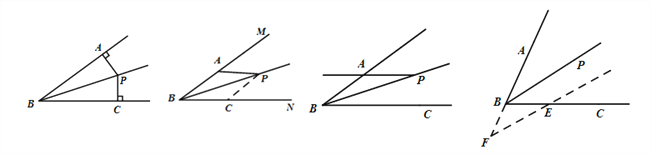
(1) (2) (3) (4)
④三線(xiàn)合一（利用角平分線(xiàn)+垂線(xiàn)→等腰三角形）：
如圖（5），已知
平分
，且
，則
， 
.
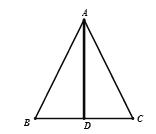
(5)
【題型】解答題
【結(jié)束】
26
【題目】如圖①，AB為半圓的直徑，O為圓心，C為圓弧上一點(diǎn)，AD垂直于過(guò)C點(diǎn)的切線(xiàn)，垂足為D，AB的延長(zhǎng)線(xiàn)交直線(xiàn)CD于點(diǎn)E.
(1)求證：AC平分∠DAB；
(2)若AB＝4，B為OE的中點(diǎn)，CF⊥AB，垂足為點(diǎn)F，求CF的長(zhǎng)；
(3)如圖②，連接OD交AC于點(diǎn)G，若
，求sinE的值．
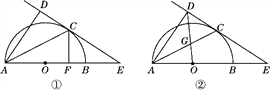
查看答案和解析>>
科目：初中數(shù)學(xué) 來(lái)源： 題型：
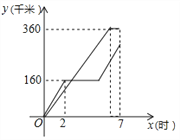
【題目】在一條公路上順次有
、
、
三地，甲、乙兩車(chē)同時(shí)從
地出發(fā)，分別勻速前往
地、
地，甲車(chē)到達(dá)
地停留一段時(shí)間后原速原路返回，乙車(chē)到達(dá)
地后立即原速原路返回，乙車(chē)比甲車(chē)早1小時(shí)返回到
地，甲、乙兩車(chē)各自行駛的路程
（千米）與時(shí)間
（小時(shí)）（從兩車(chē)出發(fā)時(shí)開(kāi)始計(jì)時(shí)）之間的函數(shù)圖像如圖所示.
（1）甲車(chē)到達(dá)
地停留的時(shí)間為 小時(shí)；
（2）求甲車(chē)返回
地的圖中
與
之間的函數(shù)關(guān)系式；
（3）直接寫(xiě)出兩車(chē)在圖中相遇時(shí)
的值.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà)：027-86699610 舉報(bào)郵箱：58377363@163.com