
【題目】對于給定的兩個“函數,任取自變量x的一個值,當x<1時,它們對應的函數值互為相反數;當x≥1時,它們對應的函數值相等,我們稱這樣的兩個函數互為相關函數.例如:一次函數y=x-4,它的相關函數為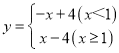 .
.
(1)一次函數y= -x+5的相關函數為______________.
(2)已知點A(b-1,4),點B坐標(b+3,4),函數y=3x-2的相關函數與線段AB有且只有一個交點,求b的取值范圍.
(3)當b+1≤x≤b+2時,函數y=-3x+b-2的相關函數的最小值為3,求b的值.
【答案】(1)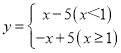 ;
;
(2)當x<1時,![]() ≤b≤
≤b≤![]() ;當x≥1時,
;當x≥1時,![]() ≤b≤
≤b≤![]() ;
;
(3)當x<1時,b=-1; 當x≥1時,b=-![]()
【解析】
(1)根據相關函數的概念可直接得出答案;
(2)由A(b-1,4),B(b+3,4)得到線段AB在直線y=4上,再求出y=3x-2的兩個相關函數的圖象與直線y=4的交點坐標,從而得到不等式,解不等式即可得出b的取值范圍.
(3)分兩種情況,當x<1時,y=-3x+b-2的相關函數是y=3x+2-b,根據一次函數的性質得到當x=b+1時,y有最小值為3,列出方程求解即可得出b值;同理,當x≥1時,y=-3x+b-2的相關函數是y=-3x+b-2, 由函數性質列出方程可得出b值.
解:(1)根據相關函數的概念可得,一次函數y= -x+5的相關函數為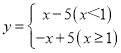 ;
;
(2)∵A(b-1,4),B(b+3,4),
∴線段AB在直線y=4上,且點A在點B的左邊,
當x<1時,y=3x-2的相關函數是y=2-3x,
把y=4代入y=2-3x,得2-3x=4,解得x=-![]()
∴直線y=4與直線y=2-3x的交點的橫坐標是x=-![]() ,
,
∴b-1≤-![]() ≤b+3
≤b+3
解得![]() ≤b≤
≤b≤![]()
當x≥1時,y=3x-2的相關函數是y=3x-2,
把y=4代入y=3x-2,得3x-2=4,解得x=2
∴直線y=4與直線y=3x-2的交點的橫坐標是x=2,
∴b-1≤2≤b+3
解得![]() ≤b≤
≤b≤![]()
綜上所述,當x<1時,![]() ≤b≤
≤b≤![]() ;當x≥1時,
;當x≥1時,![]() ≤b≤
≤b≤![]() .
.
(3)當x<1時,y=-3x+b-2的相關函數是y=3x+2-b,
∵k=3>0,y隨x的增大而增大,
∵b+1≤x≤b+2
∴當x=b+1時,y有最小值為3
∴3(b+1)+2-b=3
解得b=-1;
當x≥1時,y=-3x+b-2的相關函數是y=-3x+b-2,
∵k=-3<0,y隨x的增大而減小,
∵b+1≤x≤b+2
∴當x=b+2時,y有最小值為3
∴-3(b+2)+b-2=3
解得b=-![]()
綜上,當x<1時,b=-1; 當x≥1時,b=-![]() .
.


科目:初中數學 來源: 題型:
【題目】以下是八(1)班學生身高的統計表和扇形統計圖,請回答以下問題:
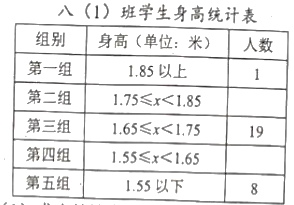
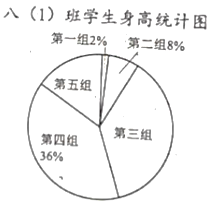
(1)求出統計表和統計圖缺的數據.
(2)八(1)班學生身高這組數據的中位數落在第幾組?
(3)如果現在八(1)班學生的平均身高是1.63m,已確定新學期班級轉來兩名新同學,新同學的身高分別是1.54m和1.77m,那么這組新數據的中位數落在第幾組?
查看答案和解析>>
科目:初中數學 來源: 題型:
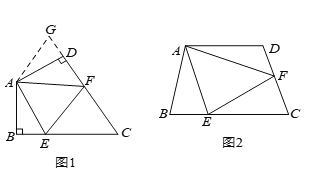
【題目】如圖(![]() ),在四邊形
),在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點,且
上的點,且![]() .探究圖中線段
.探究圖中線段![]() ,
,![]() ,
,![]() 之間的數量關系.小王同學探究此問題的方法是,延長
之間的數量關系.小王同學探究此問題的方法是,延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,先證明
,先證明![]() ≌
≌![]() ,再證明
,再證明![]() ≌
≌![]() ,可得出結論,他的結論應該是__________.
,可得出結論,他的結論應該是__________.
如圖(![]() ),若在四邊形
),若在四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 上的點,且
上的點,且![]() ,上述結論是否仍然成立,并說明理由.
,上述結論是否仍然成立,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點O為直線AB上一點,過點O作射線OC,使∠BOC=135°,將一個含45°角的直角三角板的一個頂點放在點O處,斜邊OM與直線AB重合,另外兩條直角邊都在直線AB的下方.
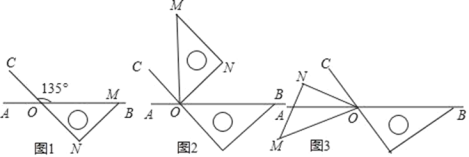
(1)將圖1中的三角板繞著點O逆時針旋轉90°,如圖2所示,此時∠BOM= ;在圖2中,OM是否平分∠CON?請說明理由;
(2)接著將圖2中的三角板繞點O逆時針繼續旋轉到圖3的位置所示,使得ON在∠AOC的內部,請探究:∠AOM與∠CON之間的數量關系,并說明理由;
(3)將圖1中的三角板繞點O按每秒4.5°的速度沿逆時針方向旋轉一周,在旋轉的過程中,當旋轉到第 秒時,∠COM與∠CON互補.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲騎自行年,乙乘坐汽車從A地出發沿同一路線勻速前往B地,甲先出發.設甲行駛的時間為x(h),甲、乙兩人距出發點的路程S甲(km)、S乙(km)關于x的函數圖象如圖1所示,甲、乙兩人之同的距離y(km)關于x的函數圖象如圖2所示,請你解決以下問題:
(1)甲的速度是__________km/h,乙的速度是_______km/h;
(2)a=_______,b=_______;
(3)甲出發多少時間后,甲、乙兩人第二次相距7.5km?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=![]() x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P時直線AC下方拋物線上的動點.
x2+bx+c經過△ABC的三個頂點,其中點A(0,1),點B(﹣9,10),AC∥x軸,點P時直線AC下方拋物線上的動點.

(1)求拋物線的解析式;(2)過點P且與y軸平行的直線l與直線AB、AC分別交于點E、F,當四邊形AECP的面積最大時,求點P的坐標;
(3)當點P為拋物線的頂點時,在直線AC上是否存在點Q,使得以C、P、Q為頂點的三角形與△ABC相似,若存在,求出點Q的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,tan∠ABC=![]() ,∠ACB=45°,AD=8,AD是邊BC上的高,垂足為D,BE=4,點M從點B出發沿BC方向以每秒3個單位的速度運動,點N從點E出發,與點M同時同方向以每秒1個單位的速度運動.以MN為邊在BC的上方作正方形MNGH.點M到達點C時停止運動,點N也隨之停止運動.設運動時間為t(秒)(t>0).
,∠ACB=45°,AD=8,AD是邊BC上的高,垂足為D,BE=4,點M從點B出發沿BC方向以每秒3個單位的速度運動,點N從點E出發,與點M同時同方向以每秒1個單位的速度運動.以MN為邊在BC的上方作正方形MNGH.點M到達點C時停止運動,點N也隨之停止運動.設運動時間為t(秒)(t>0).
(1)當t為多少秒時,點H剛好落在線段AB上?
(2)當t為多少秒時,點H剛好落在線段AC上?
(3)設正方形MNGH與Rt△ABC重疊部分的圖形的面積為S,求出S關于t的函數關系式并寫出自變量t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二青會開幕式期間,出租車司機李師傅營運時是在南北走向的濱河西路上行進的,如果規定向南為正,向北為負,他這天上午所接![]() 位乘客的行車里程(單位:
位乘客的行車里程(單位:![]() )為:
)為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .(假設相鄰兩位乘客上下車沒有時間間隔)
.(假設相鄰兩位乘客上下車沒有時間間隔)
(1)試判斷李師傅將最后一位乘客送到目的地時,他在出發點的什么方向,距離出發地多少千米?
(2)若汽車耗油量為![]() ,則這天上午李師傅接送乘客時出租車共耗油多少升?
,則這天上午李師傅接送乘客時出租車共耗油多少升?
(3)若出租車起步價為![]() 元,起步里程為
元,起步里程為![]() (包括
(包括![]() ),超過部分每千米
),超過部分每千米![]() 元,問李師傅這天上午共得車費多少元?
元,問李師傅這天上午共得車費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
在學習“可化為一元一次方程的分式方程及其解法”的過程中,老師提出一個問題:若關于x的分式方程![]() =1的解為正數,求a的取值范圍.
=1的解為正數,求a的取值范圍.
經過獨立思考與分析后,小杰和小哲開始交流解題思路如下:
小杰說:解這個關于x的分式方程,得x=a+4.由題意可得a+4>0,所以a>﹣4,問題解決.
小哲說:你考慮的不全面,還必須保證x≠4,即a+4≠4才行.
(1)請回答: 的說法是正確的,并簡述正確的理由是 ;
(2)參考對上述問題的討論,解決下面的問題:
若關于x的方程![]() 的解為非負數,求m的取值范圍.
的解為非負數,求m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com