
【題目】在平面直角坐標系中,橫坐標與縱坐標都是整數的點![]() 稱為整點,如果將二次函數
稱為整點,如果將二次函數![]() 的圖象與x軸所圍成的封閉圖形染成紅色,則此紅色區域內部及其邊界上的整點個數有______ 個
的圖象與x軸所圍成的封閉圖形染成紅色,則此紅色區域內部及其邊界上的整點個數有______ 個![]()
【答案】25
【解析】∵在![]() 中,當
中,當![]() 時,有
時,有![]() ,
,
解得:![]() ,
,
∴拋物線![]() 與
與![]() 軸的交點坐標為(6.5,0)和(1.5,0),
軸的交點坐標為(6.5,0)和(1.5,0),
∵![]() ,
,
∴拋物線![]() 的頂點坐標為(4,6.25),
的頂點坐標為(4,6.25),
∴拋物線的大致圖象如下圖所示:
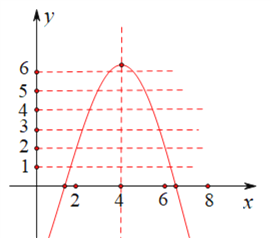
(1)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=0上,有5個符合要求的整點;
,此時,在直線y=0上,有5個符合要求的整點;
(2)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=1上,有5個符合要求的整點;
,此時,在直線y=1上,有5個符合要求的整點;
(3)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=2上,有5個符合要求的整點;
,此時,在直線y=2上,有5個符合要求的整點;
(4)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=3上,有3個符合要求的整點;
,此時,在直線y=3上,有3個符合要求的整點;
(5)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=4上,有3個符合要求的整點;
,此時,在直線y=4上,有3個符合要求的整點;
(6)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=5上,有3個符合要求的整點;
,此時,在直線y=5上,有3個符合要求的整點;
(7)當![]() 時,解得:
時,解得:![]() ,此時,在直線y=6上有1個符合要求的整點;
,此時,在直線y=6上有1個符合要求的整點;
綜上所述,共有25個整點在所圍區域內或其邊界上.


科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,點E、F在AC上,且AF=CE,點G、H分別在AB、CD上,且AG=CH,AC與GH相交于點O.
(1)求證:EG//FH;
(2)GH、EF互相平分.

查看答案和解析>>
科目:初中數學 來源: 題型:
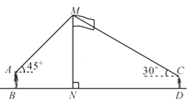
【題目】如圖,某數學興趣小組在活動課上測量學校旗桿高度.已知小明的眼睛與地面的距離(AB)是1.7 m,看旗桿頂部M的仰角為45°;小紅的眼睛與地面的距離(CD)是1.5 m,看旗桿頂部M的仰角為30°.兩人相距30米且位于旗桿兩側(點B,N,D在同一條直線上).求旗桿MN的高度.(參考數據:![]() ≈1.414,
≈1.414,![]() ≈1.732,結果保留整數)
≈1.732,結果保留整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 是直線
是直線![]() 上一點,以
上一點,以![]() 為一邊在
為一邊在![]() 的右側作
的右側作![]() ,使
,使![]() ,
,![]() ,連接
,連接![]() .設
.設![]() ,
,![]() .
.

(1)如圖(1),點![]() 在線段
在線段![]() 上移動時,試說明
上移動時,試說明![]() ;
;
(2)如圖(2),點![]() 在線段
在線段![]() 的延長線上移動時,探索角
的延長線上移動時,探索角![]() 與
與![]() 之間的數量關系并證明;
之間的數量關系并證明;
(3)當點![]() 在線段
在線段![]() 的反向延長線上移動時,請在備用圖上根據題意畫出圖形,并猜想角
的反向延長線上移動時,請在備用圖上根據題意畫出圖形,并猜想角![]() 與
與![]() 之間的數量關系是______________,線段
之間的數量關系是______________,線段![]() 、
、![]() 、
、![]() 之間的數量關系是________________.
之間的數量關系是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學為了提高綠化品位,美化環境,準備將一塊周長為114 m的長方形草地,設計成長和寬分別相等的9塊長方形(如圖所示),種上各種花卉,經市場預測,每平方米綠化費為100元.
(1)求出每個小長方形的長和寬;
(2)請計算出完成這塊草地的綠化工程預計投入資金多少元.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,直線AB與x軸、y軸的交點分別為A、![]() ,將
,將![]() 對折,使點O的對應點H恰好落在直線AB上,折痕交x軸于點C,
對折,使點O的對應點H恰好落在直線AB上,折痕交x軸于點C,
![]() 求過A、B、C三點的拋物線解析式;
求過A、B、C三點的拋物線解析式;
![]() 若拋物線的頂點為D,在直線BC上是否存在點P,使得四邊形ODAP為平行四邊形?若存在,求出點P的坐標;若不存在,說明理由;
若拋物線的頂點為D,在直線BC上是否存在點P,使得四邊形ODAP為平行四邊形?若存在,求出點P的坐標;若不存在,說明理由;
![]() 若點Q是拋物線上一個動點,使得以A、B、Q為頂點并且以AB為直角邊的直角三角形,直接寫出Q點坐標.
若點Q是拋物線上一個動點,使得以A、B、Q為頂點并且以AB為直角邊的直角三角形,直接寫出Q點坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一天,王亮同學從家里跑步到體育館,在那里鍛煉了一陣后又走到某書店去買書, 然后散步走回家如圖反映的是在這一過程中,王亮同學離家的距離 s(千米)與離家的時間 t(分鐘)之間的關系,請根據圖象解答下列問題:
(1)體育館離家的距離為 千米,書店離家的距離為_____千米;王亮同學在書店待了______分鐘.
(2)分別求王亮同學從體育館走到書店的平均速度和從書店出來散步回家的平均速度.

查看答案和解析>>
科目:初中數學 來源: 題型:
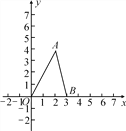
【題目】如圖,在平面直角坐標系中,點A的坐標為(2,4),點B的坐標為(3,0).三角形AOB中任意一點P(x0,y0)經平移后的對應點為P1(x0+2,y0),并且點A,O,B的對應點分別為點D,E,F.
(1)指出平移的方向和距離;
(2)畫出平移后的三角形DEF;
(3)求線段OA在平移過程中掃過的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
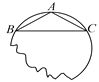
【題目】如圖,要把殘破的輪片復制完整,已知弧上的三點A、B、C.
(1)用尺規作圖法找出![]() 所在圓的圓心(保留作圖痕跡,不寫作法);
所在圓的圓心(保留作圖痕跡,不寫作法);
(2)設△ABC是等腰三角形,底邊BC=8cm,腰AB=5cm,求圓片的半徑R.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com