
【題目】如圖,函數y=ax2+bx+c的圖象過點(﹣1,0)和(m,0),請思考下列判斷:①abc<0;②4a+c<2b;③![]() =1﹣
=1﹣![]() ;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=
;④am2+(2a+b)m+a+b+c<0;⑤|am+a|=![]() 正確的是( )
正確的是( )
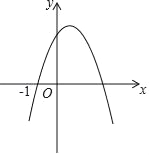
A. ①③⑤ B. ①②③④⑤ C. ①③④ D. ①②③⑤
【答案】B
【解析】
①利用圖象信息即可判斷;②根據x=-2時,y<0即可判斷;③根據m是方程ax2+bx+c=0的根,結合兩根之積-m=![]() ,即可判斷;④根據兩根之和-1+m=-
,即可判斷;④根據兩根之和-1+m=-![]() ,可得ma=a-b,可得am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,⑤根據拋物線與x軸的兩個交點之間的距離,列出關系式即可判斷.
,可得ma=a-b,可得am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,⑤根據拋物線與x軸的兩個交點之間的距離,列出關系式即可判斷.
∵拋物線開口向下,
∴a<0,
∵拋物線交y軸于正半軸,
∴c>0,
∵-![]() >0,
>0,
∴b>0,
∴abc<0,故①正確;
∵x=-2時,y<0,
∴4a-2b+c<0,即4a+c<2b,故②正確;
∵y=ax2+bx+c的圖象過點(-1,0)和(m,0),
∴-1×m=![]() ,am2+bm+c=0,
,am2+bm+c=0,
∴![]() +
+![]() +
+![]() =0,
=0,
∴![]() =1-
=1-![]() ,故③正確;
,故③正確;
∵-1+m=-![]() ,
,
∴-a+am=-b,
∴am=a-b,
∵am2+(2a+b)m+a+b+c=am2+bm+c+2am+a+b=2a-2b+a+b=3a-b<0,故④正確;
∵m+1=|![]() -
-![]() |,
|,
∴m+1=|![]() |,
|,
∴|am+a|=![]() ,故⑤正確.
,故⑤正確.
故選:B.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖①,E是AB延長線上一點,分別以AB、BE為一邊在直線AE同側作正方形ABCD和正方形BEFG,連接AG、CE.

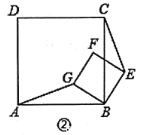
(1)試探究線段AG與CE的大小關系,并證明你的結論;
(2)若AG恰平分∠BAC,且BE=1,試求AB的長;
(3)將正方形BEFG繞點B逆時針旋轉一個銳角后,如圖②,問(1)中結論是否仍然成立,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
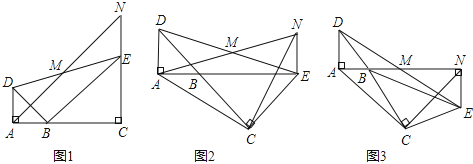
【題目】如圖,已知△BAD和△BCE均為等腰直角三角形,∠BAD=∠BCE=90°,點M為DE的中點,過點E與AD平行的直線交射線AM于點N.
(1)當A,B,C三點在同一直線上時(如圖1),求證:M為AN的中點;
(2)將圖1中的△BCE繞點B旋轉,當A,B,E三點在同一直線上時(如圖2),求證:△ACN為等腰直角三角形;
(3)將圖1中△BCE繞點B旋轉到圖3位置時,(2)中的結論是否仍成立?若成立,試證明之,若不成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了讓“兩會”精神深入青年學生,增強學子們的歷史使命和社會責任感,某高校黨委舉辦了“奮力奔跑同心追夢”兩會主題知識競答活動,文學社團為選派優秀同學參加學校競答活動,提前對甲、乙兩位同學進行了6次測驗:
①收集數據:分別記錄甲、乙兩位同學6次測驗成績(單位:分)
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
②整理數據:列表格整理兩位同學的測驗成績(單位:分)
1 | 2 | 3 | 4 | 5 | 6 | |
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
③描述數據:根據甲、乙兩位同學的成績繪制折線統計圖

④分析數據:兩組成績的平均數、中位數、眾數、方差如下表:
同學 | 平均數 | 中位數 | 眾數 | 方差 |
甲 | 84 | 82.5 | __________ | 16.3 |
乙 | 84 | 83.5 | 83 | __________ |
得出結論:結合上述統計過程,回答下列問題:
(1)補全④中表格;
(2)甲、乙兩名同學中,_______(填甲或乙)的成績更穩定,理由是______________________
(3)如果由你來選擇一名同學參加學校的競答活動,你會選擇__________(填甲或乙),理由是___________
查看答案和解析>>
科目:初中數學 來源: 題型:
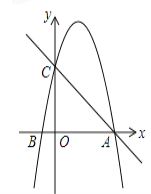
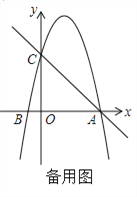
【題目】如圖,在平面直角坐標系中,已知點A 的坐標是(4,0),并且0A=OC=4OB,動點P在過A,B,C三點的拋物線上.
(1) 求拋物線的解析式;
(2)過動點P作PE垂直于y軸于點E,交直線AC于點D,過點D作x軸的垂線,垂足為F,連接EF,當線段EF的長度最短時,求出點P的坐標;
(3) 是否存在點P,使得△ACP是以AC為直角邊的直角三角形? 若存在,求出所有符合條件的點P的坐標; 若不存在,說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數的圖象與x軸交于A(﹣2,0)、B(4,0)兩點,且函數經過點(3,10).
(1)求二次函數的解析式;
(2)設這個二次函數的頂點為P,求△ABP的面積;
(3)當x為何值時,y≤0.(請直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊△ABC中,D是邊AC上一點,連接BD,將△BCD繞點B逆時針旋轉60°,得到△BAE,連接ED,若BC=5,BD=4,則以下四個結論中: ①△BDE是等邊三角形; ②AE∥BC; ③△ADE的周長是9; ④∠ADE=∠BDC.其中正確的序號是( )
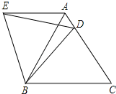
A.②③④B.①②④C.①②③D.①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(
的圖象如圖所示,以下結論:①abc>0;②4ac<b2;③2a+b>0;④其頂點坐標為(![]() ,﹣2);⑤當x<
,﹣2);⑤當x<![]() 時,y隨x的增大而減小;⑥a+b+c>0正確的有( )
時,y隨x的增大而減小;⑥a+b+c>0正確的有( )

A. 3個 B. 4個 C. 5個 D. 6個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),P為△ABC所在平面上一點,且∠APB=∠BPC=∠CPA=120°,則點P叫做△ABC的費馬點.
(1)如果點P為銳角△ABC的費馬點,且∠ABC=60°.
①求證:△ABP∽△BCP;
②若PA=3,PC=4,則PB= .
(2)已知銳角△ABC,分別以AB、AC為邊向外作正△ABE和正△ACD,CE和BD 相交于P點.如圖(2)
①求∠CPD的度數;
②求證:P點為△ABC的費馬點.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com