
【題目】如圖,在正方形ABCD中,O是對角線AC與BD的交點,M是BC邊上的動點(點M不與B、C重合),過點C作CN垂直DM交AB于點N,連結OM、ON、MN.下列五個結論:①△CNB≌△DMC;②![]() ;③ON⊥OM;④若AB=2,則
;③ON⊥OM;④若AB=2,則![]() 的最小值是1;⑤
的最小值是1;⑤![]() .其中正確結論是_________.(只填番號)
.其中正確結論是_________.(只填番號)

【答案】①②③⑤
【解析】根據正方形的性質,依次判定△CNB≌△DMC,△OCM≌△OBN,△CON≌△DOM,根據全等三角形的性質以及勾股定理進行計算即可得出結論.
∵正方形ABCD中,CD=BC,∠BCD=90°,
∴∠BCN+∠DCN=90°,
又∵CN⊥DM,
∴∠CDM+∠DCN=90°,
∴∠BCN=∠CDM,
又∵∠CBN=∠DCM=90°,
∴△CNB≌△DMC(ASA),故①正確;
根據△CNB≌△DMC,可得CM=BN,
又∵∠OCM=∠OBN=45°,OC=OB,
∴△OCM≌△OBN(SAS),
∴OM=ON,故②正確;
∵△OCM≌△OBN
∴∠COM=∠BON
∴∠COM+∠BOM=∠BON+∠BOM=90°
∴ON⊥OM
故③正確;
∵△OCM≌△OBN,
∴四邊形BMON的面積=△BOC的面積=1,即四邊形BMON的面積是定值1,
∴當△MNB的面積最大時,△MNO的面積最小,
設BN=x=CM,則BM=2-x,
∴△MNB的面積=![]() x(2-x)=-
x(2-x)=-![]() x2+x,
x2+x,
∴當x=1時,△MNB的面積有最大值![]() ,
,
此時S△OMN的最小值是1-![]() =
=![]() ,故④不正確;
,故④不正確;
∵AB=BC,CM=BN,
∴BM=AN,
又∵Rt△BMN中,BM2+BN2=MN2,
∴AN2+CM2=MN2,故⑤正確;


 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案 金狀元績優好卷系列答案
金狀元績優好卷系列答案科目:初中數學 來源: 題型:
【題目】綜合題。
(1)計算:(π﹣3.14)0+( ![]() )﹣1+|﹣2
)﹣1+|﹣2 ![]() |﹣
|﹣ ![]() .
.
(2)先化簡,再求值: ![]() ÷(
÷( ![]() ﹣x+1),并從﹣tan60°≤x≤2cos30°取出一個合適的整數,求出式子的值.
﹣x+1),并從﹣tan60°≤x≤2cos30°取出一個合適的整數,求出式子的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
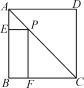
【題目】如圖,P為正方形ABCD的對角線AC上任意一點,PE⊥AB于E,PF⊥BC于F,若AC=![]() ,則四邊形PEBF的周長為( )
,則四邊形PEBF的周長為( )
A. ![]() B. 2
B. 2![]() C. 2 D. 1
C. 2 D. 1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 分別與
分別與![]() 軸、
軸、![]() 軸交于C、D兩點,與反比例函數
軸交于C、D兩點,與反比例函數![]() 的圖像相交于點
的圖像相交于點![]() 和點
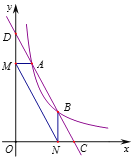
和點![]() ,過點A作AM⊥y軸于點M,過點B作BN⊥x軸于點N,連結MN、OA、OB.下列結論:
,過點A作AM⊥y軸于點M,過點B作BN⊥x軸于點N,連結MN、OA、OB.下列結論:
①![]() ;②
;②![]() ;③四邊形
;③四邊形![]() 與四邊形MNCA的周長相等;④
與四邊形MNCA的周長相等;④![]() .其中正確的個數是( )個.
.其中正確的個數是( )個.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在反比例函數y= ![]() (x>0)的圖象上有點P1、P2、P3、P4 , P5 , 它們的橫坐標依次為2,4,6,8,10,分別過這些點作x軸與y軸的垂線,圖中所構成的陰影部分的面積從左到右依次為S1 , S2 , S3 , S4 , 則S1+S2+S3+S4的值為( )
(x>0)的圖象上有點P1、P2、P3、P4 , P5 , 它們的橫坐標依次為2,4,6,8,10,分別過這些點作x軸與y軸的垂線,圖中所構成的陰影部分的面積從左到右依次為S1 , S2 , S3 , S4 , 則S1+S2+S3+S4的值為( ) 
A.4.5
B.4.2
C.4
D.3.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖1,點A、O、B依次在直線MN上,現將射線OA繞點O沿順時針方向以每秒2°的速度旋轉,同時射線OB繞點O沿逆時針方向以每秒4°的速度旋轉,如圖2,設旋轉時間為t(0秒≤t≤90秒).
(1)用含t的代數式表示∠MOA的度數.
(2)在運動過程中,當∠AOB第二次達到60°時,求t的值.
(3)在旋轉過程中是否存在這樣的t,使得射線OB是由射線OM、射線OA、射線ON中的其中兩條組成的角(指大于0°而不超過180°的角)的平分線?如果存在,請直接寫出t的值;如果不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
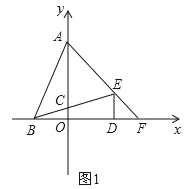
【題目】如圖,在平面直角坐標系中,點A(0,b)、B(a,0)、D(d,0),且a、b、d滿足![]() =0,DE⊥x軸且∠BED=∠ABD,BE交y軸于點C,AE交x軸于點F
=0,DE⊥x軸且∠BED=∠ABD,BE交y軸于點C,AE交x軸于點F
(1)求點A、B、D的坐標;
(2)求點E、F的坐標;
(3)如圖,點P(0,1)作x軸的平行線,在該平行線上有一點Q(點Q在點P的右側)使∠QEM=45°,QE交x軸于點N,ME交y軸的正半軸于點M,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
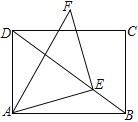
【題目】如圖,矩形ABCD中,AB=4,AD=3,E為對角線BD上一個動點,以E為直角頂點,AE為直角邊作等腰Rt△AEF,A、E、F按逆時針排列.當點E從點B運動到點D時,點F的運動路徑長為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com