【題目】如圖，反比例函數
上有一點
，點橫坐標為1，過點的直線
與
、
軸分別交于點
、點
，
.
（1）求一次函數與反比例函數的解析式；
（2）將直線沿軸方向向下平移使其過反比例函數的右支圖象上的點
，且點橫坐標為
，直線交軸于點
，連接
、
，求
.
口算心算速算應用題系列答案
同步拓展閱讀系列答案科目：初中數學 來源： 題型：
【題目】如圖，梯形ABCD中，AB∥CD，AB=14，AD= 4
， CD=7．直線l經過A，D兩點，且sin∠DAB=
． 動點P在線段AB上從點A出發以每秒2個單位的速度向點B運動，同時動點Q從點B出發以每秒5個單位的速度沿B→C→D的方向向點D運動，過點P作PM垂直于AB，與折線A→D→C相交于點M，當P，Q兩點中有一點到達終點時，另一點也隨之停止運動．設點P，Q運動的時間為t秒（t＞0），△MPQ的面積為S．
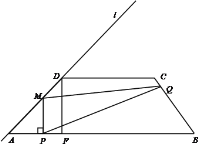
（1）求腰BC的長；
（2）當Q在BC上運動時，求S與t的函數關系式；
（3）在（2）的條件下，是否存在某一時刻t，使得△MPQ的面積S是梯形ABCD面積的
？若存在，請求出t的值；若不存在，請說明理由；
（4）隨著P，Q兩點的運動，當點M在線段DC上運動時，設PM的延長線與直線l相交于點N，試探究：當t為何值時，△QMN為等腰三角形？
查看答案和解析>>
科目：初中數學 來源： 題型：
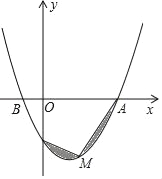
【題目】如圖，已知拋物線過點A（4，0），B（﹣2，0），C（0，﹣4）．
（1）求拋物線的解析式；
（2）如圖，點M是拋物線AC段上的一個動點，當圖中陰影部分的面積最小值時，求點M的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
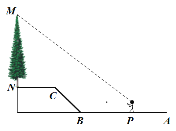
【題目】如圖，
是垂直于水平面的一棵樹，小馬（身高1.70米）從點
出發，先沿水平方向向左走10米到
點，再經過一段坡度
，坡長為5米的斜坡
到達
點，然后再沿水平方向向左行走5米到達
點（、、、在同一平面內），小馬在線段
的黃金分割點
處（
）測得大樹的頂端
的仰角為37°，則大樹的高度約為（ ）米.（參考數據：
）
A. 7.8米 B. 8.0米 C. 8.1米 D. 8.3米
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D為BC的中點，若動點E以1cm/s的速度從A點出發，沿著A→B→A的方向運動，設E點的運動時間為t秒（0≤t＜6），連接DE，當△BDE是直角三角形時，t的值為
A、2 B、2.5或3.5 C、3.5或4.5 D、2或3.5或4.5
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ACDE是證明勾股定理時用到的一個圖形，a、b、c是Rt△ABC和Rt△BED邊長，易知AE=
c，這時我們把關于x的形如ax+
cx+b=0的一元二次方程稱為“勾系一元二次方程”.
請解決下列問題：
寫出一個“勾系一元二次方程”；
求證：關于x的“勾系一元二次方程”ax+
cx+b=0必有實數根；
若x=1是“勾系一元二次方程”ax+
cx+b=0的一個根，且四邊形ACDE的周長是
，求△ABC面積.
查看答案和解析>>
科目：初中數學 來源： 題型：
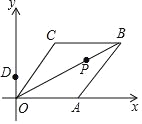
【題目】如圖，已知菱形OABC的邊OA在x軸上，點B的坐標為（8，4），P是對角線OB上的一個動點，點D（0，1）在y軸上，當PC+PD最短時，最短距離是_____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】觀察與思考：閱讀下列材料，并解決后面的問題
在銳角△ABC中，∠A、∠B、∠C的對邊分別是a、b、c，過A作AD⊥BC于D（如圖(1)），則sinB=
，sinC=
，即AD＝csinB，AD＝bsinC，于是csinB＝bsinC，即
，同理有：
，
，所以
．
即：在一個三角形中，各邊和它所對角的正弦的比相等在銳角三角形中，若已知三個元素（至少有一條邊），運用上述結論和有關定理就可以求出其余三個未知元素．
根據上述材料，完成下列各題．
(1)如圖(2)，△ABC中，∠B＝45°，∠C＝75°，BC＝60，則∠A＝ ；AC＝ ；
(2)自從去年日本政府自主自導“釣魚島國有化”鬧劇以來，我國政府靈活應對，現如今已對釣魚島執行常態化巡邏．某次巡邏中，如圖（3），我漁政204船在C處測得A在我漁政船的北偏西30°的方向上，隨后以40海里/時的速度按北偏東30°的方向航行，半小時后到達B處，此時又測得釣魚島A在的北偏西75°的方向上，求此時漁政204船距釣魚島A的距離AB．（結果精確到0.01，
≈2.449）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
