
【題目】在菱形![]() 中,對角線
中,對角線![]() ,
,![]() 交于點
交于點![]() ,
,![]() 為
為![]() 上點,且
上點,且![]() ,
,![]() 為
為![]() 上點,
上點,![]() 為
為![]() 上點,且
上點,且![]() ,并與
,并與![]() 相交于點
相交于點![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的長.(結果用
的長.(結果用![]() 表示)
表示)
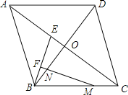
【答案】![]() 證明見解析;(2)
證明見解析;(2)![]()
【解析】
(1)由菱形性質得AC⊥BD,由已知得出∠CEB=∠CBE,由MF⊥BE,得出∠BOE=∠BFM,即可得出結論;
(2)作MP∥AC于BE交于點P,與OB交于點Q,由△BOE∽△MFB,得出∠EBO=∠FMB,證出tan∠OCB=![]() ,由平行線的性質得出∠MPB=∠CEB=∠CBE,∠MQN=90°,
,由平行線的性質得出∠MPB=∠CEB=∠CBE,∠MQN=90°,![]() ,證出△MBP為等腰三角形,由等腰三角形的三線合一性質得出BF=FP,∠PMF=∠BMF=∠PBQ,證得△PBQ∽△NMQ,由對應邊成比例得出比例式即可求出結果.
,證出△MBP為等腰三角形,由等腰三角形的三線合一性質得出BF=FP,∠PMF=∠BMF=∠PBQ,證得△PBQ∽△NMQ,由對應邊成比例得出比例式即可求出結果.
![]() ) ∵
) ∵![]() 、
、![]() 是菱形
是菱形![]() 的對角線,
的對角線,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
![]() 作
作![]() 與
與![]() 交于點
交于點![]() ,與
,與![]() 交于點
交于點![]() ,如圖所示:
,如圖所示:
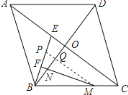
由![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() 為等腰三角形,
為等腰三角形,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()


科目:初中數學 來源: 題型:
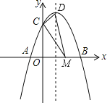
【題目】如圖,對稱軸為![]() 的拋物線
的拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,其中
點,其中![]() 點坐標為
點坐標為![]() 設拋物線的頂點為
設拋物線的頂點為![]() .
.
![]() 求拋物線的解析式及頂點坐標;
求拋物線的解析式及頂點坐標;
![]() 為
為![]() 軸上的一點,當
軸上的一點,當![]() 的周長最小時,求點
的周長最小時,求點![]() 的坐標及
的坐標及![]() 的周長.
的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中,點E是邊CD的中點,將△ADE沿AE折疊得到△AFE,且點F在長方形ABCD內.將AF延長交邊BC于點G.若BG=3CG,則![]() =( )
=( )

A.![]() B.1C.
B.1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進甲、乙兩種商品,甲種商品共用了![]() 元,乙種商品共用了
元,乙種商品共用了![]() 元.已知乙種商品每件進價比甲種商品每件進價多
元.已知乙種商品每件進價比甲種商品每件進價多![]() 元,且購進的甲、乙兩種商品件數相同.
元,且購進的甲、乙兩種商品件數相同.
![]() 求甲、乙兩種商品的每件進價;
求甲、乙兩種商品的每件進價;
![]() 該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為
該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為![]() 元,乙種商品的銷售單價為
元,乙種商品的銷售單價為![]() 元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的九折銷售;乙種商品銷售單價保持不變.要使兩種商品全部售完后共獲利不少于
元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的九折銷售;乙種商品銷售單價保持不變.要使兩種商品全部售完后共獲利不少于![]() 元,問甲種商品按原銷售單價至少銷售多少件?
元,問甲種商品按原銷售單價至少銷售多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,過點D作DF⊥BC,垂足為F,DF與AC交于點M,已知∠1=∠2.
(1)求證:CM=DM;
(2)若FB=FC,求證:AM-MD=2FM.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ABC=∠ACB,把這個三角形折疊,使得點B與點A重合,折痕分別交直線AB,AC于點M,N,若∠ANM=50°,則∠B的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
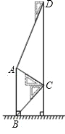
【題目】如圖,某中學在教學樓前新建了一座雕塑![]() .為了測量雕塑的高度,小明在二樓找到一點
.為了測量雕塑的高度,小明在二樓找到一點![]() ,利用三角尺測得雕塑頂端點
,利用三角尺測得雕塑頂端點![]() 的仰角為
的仰角為![]() ,底部點
,底部點![]() 的俯角為
的俯角為![]() ,小華在五樓找到一點
,小華在五樓找到一點![]() ,利用三角尺測得點
,利用三角尺測得點![]() 的俯角為
的俯角為![]() .若
.若![]() 為
為![]() ,則雕塑
,則雕塑![]() 的高度為________
的高度為________![]() .(結果精確到
.(結果精確到![]() ,參考數據:
,參考數據:![]() ).
).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1的解析表達式為y=-![]() x-1,且l1與x軸交于點D,直線l2經過定點A(2,0),B(-1,3),直線l1與l2交于點C.
x-1,且l1與x軸交于點D,直線l2經過定點A(2,0),B(-1,3),直線l1與l2交于點C.

(1)求直線l2的函數關系式;
(2)求△ADC的面積;
(3)在直線l2上存在異于點C的另一點P,使得△ADP與△ADC的面積相等,請寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y=ax2+bx+c與x軸交于A,B兩點,頂點C的縱坐標為﹣2,現將拋物線向右平移2個單位,得到拋物線y=a1x2+b1x+c1,則下列結論:①b>0;②a﹣b+c<0;③陰影部分的面積為4;④若c=﹣1,則b2=4a.其中正確的個數為( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com