
【題目】如圖,直線l1的解析表達(dá)式為y=-![]() x-1,且l1與x軸交于點(diǎn)D,直線l2經(jīng)過(guò)定點(diǎn)A(2,0),B(-1,3),直線l1與l2交于點(diǎn)C.
x-1,且l1與x軸交于點(diǎn)D,直線l2經(jīng)過(guò)定點(diǎn)A(2,0),B(-1,3),直線l1與l2交于點(diǎn)C.

(1)求直線l2的函數(shù)關(guān)系式;
(2)求△ADC的面積;
(3)在直線l2上存在異于點(diǎn)C的另一點(diǎn)P,使得△ADP與△ADC的面積相等,請(qǐng)寫(xiě)出點(diǎn)P的坐標(biāo).
【答案】(1)l2的函數(shù)關(guān)系式為:y=-x+2;(2)8;(3)P點(diǎn)坐標(biāo)為:(-2,4).
【解析】
試題(1)設(shè)l2的函數(shù)關(guān)系式為:y=kx+b,再把A(2,0),B(-1,3)代入可得關(guān)于k、b的方程組,再解方程組即可得到k、b的值,進(jìn)而可得函數(shù)解析式;
(2)聯(lián)立l1和l2的解析式,再解方程組可得C點(diǎn)坐標(biāo),再利用直線l1的解析式計(jì)算出D點(diǎn)坐標(biāo),進(jìn)而可得△ADC的面積;
(3)根據(jù)△ADP與△ADC的面積相等可得△ADP的面積為8,再由AD=4,計(jì)算出P點(diǎn)縱坐標(biāo),再利用l2的解析式確定橫坐標(biāo),進(jìn)而可得答案.
試題解析:(1)設(shè)l2的函數(shù)關(guān)系式為:y=kx+b,
∵直線過(guò)A(2,0),B(-1,3),
∴![]() ,解得:
,解得:![]() ,
,
∴l(xiāng)2的函數(shù)關(guān)系式為:y=-x+2;
(2)∵l1的解析表達(dá)式為y=-![]() x-1,
x-1,
∴D點(diǎn)坐標(biāo)是(-2,0),
∵直線l1與l2交于點(diǎn)C.
∴ ,解得
,解得![]() ,
,
∴C(6,-4),
△ADC的面積為:![]() ×AD×4=
×AD×4=![]() ×4×4=8;
×4×4=8;
(3)∵△ADP與△ADC的面積相等,
∴△ADP的面積為8,
∵AD長(zhǎng)是4,
∴P點(diǎn)縱坐標(biāo)是4,
再根據(jù)P在l2上,則4=-x+2,解得:x=-2,
故P點(diǎn)坐標(biāo)為:(-2,4).


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在正方形ABCD外取一點(diǎn)E,連接AE,BE,DE,過(guò)點(diǎn)A作AE的垂線交DE于點(diǎn)P.若AE=AP=1,PB=![]() .下列結(jié)論:①△APD≌△AEB;②點(diǎn)B到直線AE的距離為
.下列結(jié)論:①△APD≌△AEB;②點(diǎn)B到直線AE的距離為![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() .其中正確結(jié)論的序號(hào)是( )
.其中正確結(jié)論的序號(hào)是( )
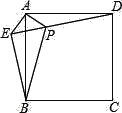
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
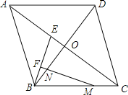
【題目】在菱形![]() 中,對(duì)角線
中,對(duì)角線![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() 為
為![]() 上點(diǎn),且
上點(diǎn),且![]() ,
,![]() 為
為![]() 上點(diǎn),
上點(diǎn),![]() 為
為![]() 上點(diǎn),且
上點(diǎn),且![]() ,并與
,并與![]() 相交于點(diǎn)
相交于點(diǎn)![]() .
.
![]() 求證:
求證:![]() ;
;
![]() 若
若![]() ,
,![]() ,求
,求![]() 的長(zhǎng).(結(jié)果用
的長(zhǎng).(結(jié)果用![]() 表示)
表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,將一張矩形紙片ABCD沿直線MN折疊,使點(diǎn)C落在點(diǎn)A處,點(diǎn)D落在點(diǎn)E處,直線MN交BC于點(diǎn)M,交AD于點(diǎn)N.
(1)求證:CM=CN;
(2)若△CMN的面積與△CDN的面積比為3:1,且CD=4,求線段MN的長(zhǎng).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在如圖所示的正方形網(wǎng)格中,每個(gè)小正方形的邊長(zhǎng)為1,格點(diǎn)三角形(頂點(diǎn)是網(wǎng)格線的交點(diǎn)的三角形)![]() 的頂點(diǎn)A、C的坐標(biāo)分別為(-4,3)、(-1,1).
的頂點(diǎn)A、C的坐標(biāo)分別為(-4,3)、(-1,1).
(1)請(qǐng)?jiān)谌鐖D所示的網(wǎng)格平面內(nèi)作出平面直角坐標(biāo)系;
(2)請(qǐng)作出![]() 關(guān)于y對(duì)稱(chēng)的△A′B′C′;
關(guān)于y對(duì)稱(chēng)的△A′B′C′;
(3)寫(xiě)出點(diǎn)![]() 的坐標(biāo) ;
的坐標(biāo) ;![]() 的面積為 .
的面積為 .
(4)若在y軸上有點(diǎn)M,則能使△ABM的周長(zhǎng)最小的點(diǎn)M的坐標(biāo)為 .

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,△ABC是等邊三角形,D點(diǎn)是AC的中點(diǎn),延長(zhǎng)BC到E,使CE=CD.

(1)用尺規(guī)作圖的方法,過(guò)D點(diǎn)作DM⊥BE,垂足是M(不寫(xiě)作法,保留作圖痕跡);
(2)求證:BM=EM.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市積極開(kāi)展“陽(yáng)光體育進(jìn)校園”活動(dòng),各校學(xué)生堅(jiān)持每天鍛煉一小時(shí),某校根據(jù)實(shí)際,決定主要開(kāi)設(shè)A:乒乓球,B:籃球,C:跑步,D:跳繩四種運(yùn)動(dòng)項(xiàng)目,為了解學(xué)生最喜歡哪一種項(xiàng)目,隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查,并將調(diào)查結(jié)果繪制成如下統(tǒng)計(jì)圖.請(qǐng)你結(jié)合圖中信息解答下列問(wèn)題.

(1)請(qǐng)計(jì)算最喜歡B項(xiàng)目的人數(shù)所占的百分比.
(2)請(qǐng)計(jì)算D項(xiàng)所在扇形圖中的圓心角的度數(shù).
(3)請(qǐng)把統(tǒng)計(jì)圖補(bǔ)充完整.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
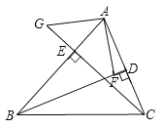
【題目】如圖,![]() 、
、![]() 是
是![]() 的高,
的高,![]() 、
、![]() 垂足,在
垂足,在![]() 上截取
上截取![]() ,使
,使![]() ,在
,在![]() 的延長(zhǎng)線取一點(diǎn)
的延長(zhǎng)線取一點(diǎn)![]() ,使
,使![]() .試說(shuō)明:①
.試說(shuō)明:①![]() ;②
;②![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,四邊形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求證:BD⊥CB;
(2)求四邊形 ABCD 的面積;
(3)如圖 2,以 A 為坐標(biāo)原點(diǎn),以 AB、AD所在直線為 x軸、y軸建立直角坐標(biāo)系,
點(diǎn)P在y軸上,若 S△PBD=![]() S四邊形ABCD,求 P的坐標(biāo).
S四邊形ABCD,求 P的坐標(biāo).

查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com