
【題目】崇左市江州區太平鎮壺城社區調查居民雙休日的學習狀況,采取了下列調查方式;a:從崇左高中、太平鎮中、太平小學三所學校中選取200名教師;b:從不同住宅樓(即江灣花園與萬鵬住宅樓)中隨機選取200名居民;c:選取所管轄區內學校的200名在校學生.并將最合理的調查方式得到的數據制成扇形統計圖和部分數據的頻數分布直方圖.以下結論:①上述調查方式最合理的是b;②在這次調查的200名教師中,在家學習的有60人;③估計該社區2000名居民中雙休日學習時間不少于4小時的人數是1180人;④小明的叔叔住在該社區,那么雙休日他去叔叔家時,正好叔叔不學習的概率是0.1.其中正確的結論是( ) 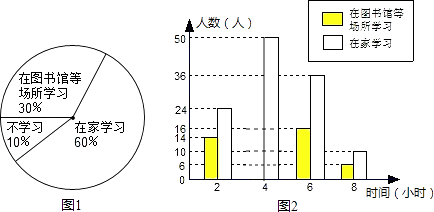
A.①④
B.②④
C.①③④
D.①②③④
【答案】A
【解析】解:①正確; ②錯誤,在家學習的人數=200×60%=120人;
③錯誤,在圖書館學習的人數=200×30%=60人,其中在圖書館學習有4小時的人數=60﹣14﹣16﹣6=24人,
則2000人中雙休日學習時間不少于4小時的人數=2000×[(24+50+16+36+6+10)÷200]=1420人;
④正確,根據扇形統計圖可得不學習的概率是10%,故正好叔叔不學習的概率是0.1.
故選A.
【考點精析】解答此題的關鍵在于理解頻數分布直方圖的相關知識,掌握特點:①易于顯示各組的頻數分布情況;②易于顯示各組的頻數差別.(注意區分條形統計圖與頻數分布直方圖),以及對扇形統計圖的理解,了解能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
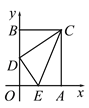
【題目】如圖,在平面直角坐標系中,矩形OACB的頂點O是坐標原點,頂點A、B分別在x軸、y軸的正半軸上,OA=3,OB=4,D為邊OB的中點.若E為邊OA上的一個動點,當△CDE的周長最小時,則點E的坐標____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角梯形ABCD中,AD∥BC,∠C=90°,AD=5,BC=9,以A為中心將腰AB順時針旋轉90°至AE,連接DE,則△ADE的面積等于( )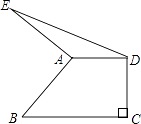
A.10
B.11
C.12
D.13
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農場急需銨肥8噸,在該農場南北方向分別有一家化肥公司A、B,A公司有銨肥3噸,每噸售價750元;B公司有銨肥7噸,每噸售價700元,汽車每千米的運輸費用b(單位:元/千米)與運輸重量a(單位:噸)的關系如圖所示.

(1)根據圖象求出b關于a的函數解析式(包括自變量的取值范圍);
(2)若農場到B公司的路程是農場到A公司路程的2倍,農場到A公司的路程為m千米,設農場從A公司購買x噸銨肥,購買8噸銨肥的總費用為y元(總費用=購買銨肥費用+運輸費用),求出y關于x的函數解析式(m為常數),并向農場建議總費用最低的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=ax2+bx+3的頂點為M(2,﹣1),交x軸于點A、B兩點,交y軸于點C,其中點B的坐標為(3,0).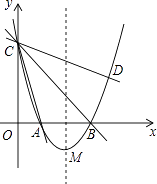
(1)求拋物線的解析式;
(2)設經過點C的直線與該拋物線的另一個點為D,且直線CD和直線CA關于直線CB對稱,求直線CD的解析式;
(3)在該拋物線的對稱軸上存在點P,滿足PM2+PB2+PC2=35,求點P的坐標;并直接寫出此時直線OP與該拋物線交點的個數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)開學初,小明到文具批發部一次性購買某種筆記本,該文具批發部規定:這種筆記本售價y(元/本)與購買數量x(本)之間的函數關系如圖所示.
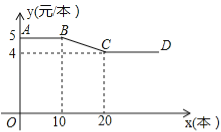
(1)圖中線段AB所表示的實際意義是 ;
(2)請直接寫出y與x之間的函數關系式;
(3)已知該文具批發部這種筆記本的進價是3元/本,若小明購買此種筆記本超過10本但不超過20本,那么小明購買多少本時,該文具批發部在這次買賣中所獲的利潤W(元)最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為1,其中弧DE、弧EF、弧FG的圓心依次為點A、B、C. 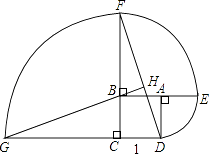
(1)求點D沿三條弧運動到點G所經過的路線長;
(2)判斷直線GB與DF的位置關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=6,AB=4,點E、G、H、F分別在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,點P是直線EF、GH之間任意一點,連接PE、PF、PG、PH,則PEF和PGH的面積和等于.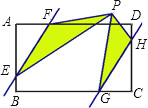
查看答案和解析>>
科目:初中數學 來源: 題型:
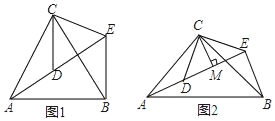
【題目】(1)問題探究:如圖1,△ACB和△DCE均為等邊三角形,點A、D、E在同一直線上,連接BE.
①求證:△CDA≌△CEB;
②求∠AEB的度數.
(2)問題變式:如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點A、D、E在同一直線上,CM為△DCE中DE邊上的高,連接BE.
①請求出∠AEB的度數
②直接寫出線段AE、CM、BE之間的數量關系,不必說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com