
【題目】某課題研究小組就圖形面積問題進行專題研究,他們發現如下結論: ①有一條邊對應相等的兩個三角形面積之比等于這條邊上的對應高之比;
②有一個角對應相等的兩個三角形面積之比等于夾這個角的兩邊乘積之比;
…
現請你繼續對下面問題進行探究,探究過程可直接應用上述結論.(S表示面積)
問題1:如圖1,現有一塊三角形紙板ABC,P1 , P2三等分邊AB,R1 , R2三等分邊AC.經探究知 ![]() =
= ![]() S△ABC , 請證明.
S△ABC , 請證明.
問題2:若有另一塊三角形紙板,可將其與問題1中的拼合成四邊形ABCD,如圖2,Q1 , Q2三等分邊DC.請探究 ![]() 與S四邊形ABCD之間的數量關系.
與S四邊形ABCD之間的數量關系.
問題3:如圖3,P1 , P2 , P3 , P4五等分邊AB,Q1 , Q2 , Q3 , Q4五等分邊DC.若S四邊形ABCD=1,求 ![]() .
.
問題4:如圖4,P1 , P2 , P3四等分邊AB,Q1 , Q2 , Q3四等分邊DC,P1Q1 , P2Q2 , P3Q3將四邊形ABCD分成四個部分,面積分別為S1 , S2 , S3 , S4 . 請直接寫出含有S1 , S2 , S3 , S4的一個等式.
【答案】解:問題1,證明: 如圖1,連接P1R2 , R2B,在△AP1R2中,∵P1R1為中線,∴S△AP1R1=S△P1R1R2 ,
同理S△P1R2P2=S△P2R2B ,
∴S△P1R1R2+S△P1R2P2= ![]() S△ABR2=S四邊形P1P2R2R1 ,
S△ABR2=S四邊形P1P2R2R1 ,
由R1 , R2為AC的三等分點可知,S△BCR2= ![]() S△ABR2 ,
S△ABR2 ,
∴S△ABC=S△BCR2+S△ABR2=S四邊形P1P2R2R1+2S四邊形P1P2R2R1=3S四邊形P1P2R2R1 ,
∴S四邊形P1P2R2R1= ![]() S△ABC;
S△ABC;
問題2,S四邊形ABCD=3S四邊形P1Q1Q2P2 .
理由:如圖2,連接AQ1 , Q1P2 , P2C,在△AQ1P2中,∵Q1P1為中線,
∴S△AQ1P1=S△P1Q1P2 , 同理S△P2Q1Q2=S△P2Q2C ,
∴S△P1Q1P2+S△P2Q1Q2= ![]() S四邊形AQ1CP2=S四邊形P1Q1Q2P2 ,
S四邊形AQ1CP2=S四邊形P1Q1Q2P2 ,
由Q1 , P2為CD,AB的三等分點可知,S△ADQ1= ![]() S△AQ1C , S△BCP2=
S△AQ1C , S△BCP2= ![]() S△AP2C ,
S△AP2C ,
∴S△ADQ1+S△BCP2= ![]() (S△AQ1C+S△AP2C)=
(S△AQ1C+S△AP2C)= ![]() S四邊形AQ1CP2 ,
S四邊形AQ1CP2 ,
∴S四邊形ABCD=S△ADC+S△ABC=S四邊形AQ1CP2+S△ADQ1+S△BCP2=3S四邊形P1Q1Q2P2 ,
即S四邊形ABCD=3S四邊形P1Q1Q2P2;
問題3,解:
如圖3,由問題2的結論可知,3S2=S1+S2+S3 , 即2S2=S1+S3 , 同理得2S3=S2+S4 , 2S4=S3+S5 ,
三式相加得,S2+S4=S1+S5 ,
∴S1+S2+S3+S4+S5=2(S2+S4)+S3=2×2S3+S3=5S3 , 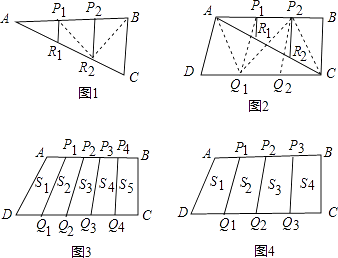
即S四邊形P2Q2Q3P3= ![]() S四邊形ABCD=
S四邊形ABCD= ![]() ;
;
問題4,如圖4,關系式為:S2+S3=S1+S4
【解析】問題1,圖1中,連接P1R2 , R2B,由三角形中線的性質得S△AP1R1=S△P1R1R2 , S△P1R2P2=S△P2R2B , 再由R1 , R2為AC的三等分點,得S△BCR2= ![]() S△ABR2 , 根據圖形的面積關系,得S△ABC與S四邊形P1P2R2R1的數量關系,證明結論; 問題2,圖2中,連接AQ1 , Q1P2 , P2C,由三角形的中線性質,得S△AQ1P1=S△P1Q1P2 , S△P2Q1Q2=S△P2Q2C , 由Q1 , P2為CD,AB的三等分點可知,S△ADQ1=
S△ABR2 , 根據圖形的面積關系,得S△ABC與S四邊形P1P2R2R1的數量關系,證明結論; 問題2,圖2中,連接AQ1 , Q1P2 , P2C,由三角形的中線性質,得S△AQ1P1=S△P1Q1P2 , S△P2Q1Q2=S△P2Q2C , 由Q1 , P2為CD,AB的三等分點可知,S△ADQ1= ![]() S△AQ1C , S△BCP2=
S△AQ1C , S△BCP2= ![]() S△AP2C , 得出S△ADQ1+S△BCP2與S四邊形AQ1CP2的關系,再根據圖形的面積關系,得S四邊形ABCD與S四邊形P1Q1Q2P2的等量關系;
S△AP2C , 得出S△ADQ1+S△BCP2與S四邊形AQ1CP2的關系,再根據圖形的面積關系,得S四邊形ABCD與S四邊形P1Q1Q2P2的等量關系;
問題3,圖3中,依次設四邊形的面積為S1 , S2 , S3 , S4 , S5 , 由問題2的結論可推出2S2=S1+S3 , 2S3=S2+S4 , 2S4=S3+S5 , 三式相加,得S2+S4=S1+S5 , 利用換元法求S1+S2+S3+S4+S5與S3的數量關系,已知S四邊形ABCD=1,可求S四邊形P2Q2Q3P3;
問題4,圖4中,由問題2的結論可知,2S2=S1+S3 , 2S3=S2+S4 , 兩式相加得S1 , S2 , S3 , S4的等量關系.
【考點精析】解答此題的關鍵在于理解三角形的面積的相關知識,掌握三角形的面積=1/2×底×高.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,∠BAC=36°,

(1)作出AB邊的垂直平分線DE,交AC于點D,交AB于點E,連接BD;
(2)下列結論正確的是:
① BD平分∠ABC;② AD=BD=BC;③ △BDC的周長等于AB+BC; ④ D點是AC中點;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系xOy中,一次函數y=﹣ ![]() x+b(b為常數,b>0)的圖象與x軸、y軸分別相交于點A、B,半徑為4的⊙O與x軸正半軸相交于點C,與y軸相交于點D、E,點D在點E上方.
x+b(b為常數,b>0)的圖象與x軸、y軸分別相交于點A、B,半徑為4的⊙O與x軸正半軸相交于點C,與y軸相交于點D、E,點D在點E上方. 
(1)若直線AB與 ![]() 有兩個交點F、G. ①求∠CFE的度數;
有兩個交點F、G. ①求∠CFE的度數;
②用含b的代數式表示FG2 , 并直接寫出b的取值范圍;
(2)設b≥5,在線段AB上是否存在點P,使∠CPE=45°?若存在,請求出P點坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=a(x2﹣2mx﹣3m2)(其中a,m是常數,且a>0,m>0)的圖象與x軸分別交于點A、B(點A位于點B的左側),與y軸交于C(0,﹣3),點D在二次函數的圖象上,CD∥AB,連接AD,過點A作射線AE交二次函數的圖象于點E,AB平分∠DAE.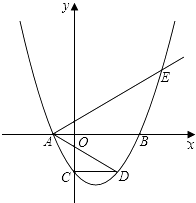
(1)用含m的代數式表示a;
(2)求證: ![]() 為定值;
為定值;
(3)設該二次函數圖象的頂點為F,探索:在x軸的負半軸上是否存在點G,連接GF,以線段GF、AD、AE的長度為三邊長的三角形是直角三角形?如果存在,只要找出一個滿足要求的點G即可,并用含m的代數式表示該點的橫坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,自來水廠A和村莊B在小河l的兩側,現要在A,B間鋪設一條輸水管道.為了搞好工程預算,需測算出A,B間的距離.一小船在點P處測得A在正北方向,B位于南偏東24.5°方向,前行1200m,到達點Q處,測得A位于北偏西49°方向,B位于南偏西41°方向.
(1)線段BQ與PQ是否相等?請說明理由;
(2)求A,B間的距離.(參考數據cos41°≈0.75)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,P(m,m)是反比例函數y= ![]() 在第一象限內的圖象上一點,以P為頂點作等邊△PAB,使AB落在x軸上,則△POB的面積為( )
在第一象限內的圖象上一點,以P為頂點作等邊△PAB,使AB落在x軸上,則△POB的面積為( ) 
A.![]()
B.3 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】江漢平原享有“中國小龍蝦之鄉”的美稱,甲、乙兩家農貿商店,平時以同樣的價格出售品質相同的小龍蝦,“龍蝦節”期間,甲、乙兩家商店都讓利酬賓,付款金額y甲、y乙(單位:元)與原價x(單位:元)之間的函數關系如圖所示: 
(1)直接寫出y甲 , y乙關于x的函數關系式;
(2)“龍蝦節”期間,如何選擇甲、乙兩家商店購買小龍蝦更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個幾何體的主視圖和俯視圖如圖所示,若這個幾何體最多有a個小正方體組成,最少有b個小正方體組成,則a+b等于( ) 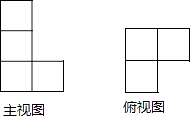
A.10
B.11
C.12
D.13
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com