
【題目】如圖,在△ABC中,BA=BC,以AB為直徑作⊙O,交AC于點D,連接DB,過點D作DE⊥BC,垂足為E.
(1)求證:AD=CD.
(2)求證:DE為⊙O的切線.
(3)若∠C=60°,DE=![]() ,求⊙O半徑的長.
,求⊙O半徑的長.
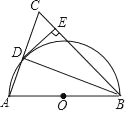
【答案】(1)詳見解析;(2)詳見解析;(3)⊙O半徑的長為4.
【解析】
(1)先利用圓周角定理得到∠ADB=90°,再根據等腰三角形的性質得AD=CD;
(2)連接OD,如圖,先證明OD為△BAC的中位線,則OD∥BC,再利用DE⊥BC得到OD⊥DE,然后根據切線的判定定理得到結論;
(3)先在Rt△CDE中計算出CE=![]() DE=2,CD=2CE=4,再利用∠A=∠C=60°,AD=CD=4,然后在Rt△ADB中利用AB=2AD求解.
DE=2,CD=2CE=4,再利用∠A=∠C=60°,AD=CD=4,然后在Rt△ADB中利用AB=2AD求解.
(1)證明:∵AB為直徑,
∴∠ADB=90°,
∵BA=BC,
∴AD=CD;
(2)證明:連接OD,如圖,
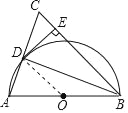
∵AD=CD,AO=OB,
∴OD為△BAC的中位線,
∴OD∥BC,
∴DE⊥BC,
∴OD⊥DE,
∴DE為⊙O的切線;
(3)在Rt△CDE中,∠C=60°,DE=![]() ,
,
∴CE=![]() DE=
DE=![]() ×2
×2![]() =2,
=2,
∴CD=2CE=4,
∵∠A=∠C=60°,AD=CD=4,
在Rt△ADB中,AB=2AD=8,
即⊙O半徑的長為4.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DEF中,已有條件AB=DE,還需要添加兩個條件才能使△ABC≌△DEF.不能添加的一組條件是( )

A. ∠B=∠E,BC=EF B. ∠A=∠D,BC=EF
C. ∠A=∠D,∠B=∠E D. BC=EF,AC=DF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,對角線AC,BD相交于點O,∠ADB=30°,E為BC邊上一點,∠AEB=45°,CF⊥BD于F.下列結論:①BE=CD,②BF=3DF,③AE=![]() AO,④CE=CF.正確的結論有( )
AO,④CE=CF.正確的結論有( )
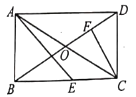
A. ①②B. ②③C. ①②④D. ①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
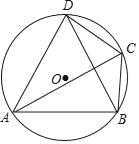
【題目】如圖,在⊙O的內接四邊形ABCD中,∠BCD=120°,CA平分∠BCD.
(1)求證:△ABD是等邊三角形;
(2)若BD=3,求⊙O的半徑.
查看答案和解析>>
科目:初中數學 來源: 題型:
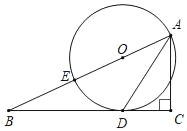
【題目】如圖,已知點E在△ABC的邊AB上,∠C=90°,∠BAC的平分線交BC于點D,且D在以A為直徑的⊙O上.
(1)求證:BC是⊙O的切線;
(2)若DC=4,AC=6,求圓心O到AD的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
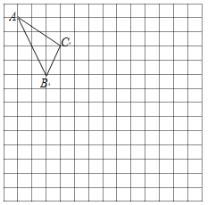
【題目】如圖,在正方形網格中,每一個小正方形的邊長為1.△ABC的三個頂點都在格點上,A、C的坐標分別是(﹣4,6),(﹣1,4).
(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出△ABC向右平移6個單位的△A1B1C1,并寫出C1的坐標 ;
(3)請畫出△ABC關于原點O對稱的△A2B2C2 , 并寫出點C2的坐標 .
查看答案和解析>>
科目:初中數學 來源: 題型:
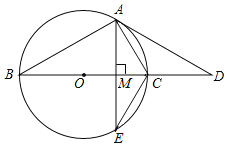
【題目】已知BC是⊙O的直徑,點D是BC延長線上一點,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求證:直線AD是⊙O的切線;
(2)若AE⊥BC,垂足為M,⊙O的半徑為4,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
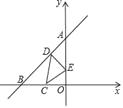
【題目】如圖所示,直線 y=x+2 與兩坐標軸分別交于A、B 兩點,點 C 是 OB 的中點,D、E 分 別是直線 AB、y 軸上的動點,則△CDE 周長的最小值是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形![]() 中,
中,![]() 是對角線
是對角線![]() 上一個動點,連結
上一個動點,連結![]() ,過
,過![]() 作
作![]() ,
,![]() ,
,
![]() ,
,![]() 分別為垂足.
分別為垂足.
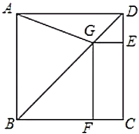
(1)求證:![]() ;
;
(2)①寫出![]() 、
、![]() 、
、![]() 三條線段滿足的等量關系,并證明;②求當
三條線段滿足的等量關系,并證明;②求當![]() ,
,![]() 時,
時,![]() 的長
的長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com