
【題目】張老師在講解復習《圓》的內容時,用投影儀屏幕展示出如下內容:
如圖,![]() 內接于
內接于![]() ,直徑
,直徑![]() 的長為2,過點
的長為2,過點![]() 的切線交
的切線交![]() 的延長線于點
的延長線于點![]() .
.
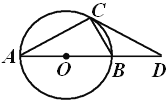
張老師讓同學們添加條件后,編制一道題目,并按要求完成下列填空.
(1)在屏幕內容中添加條件![]() ,則
,則![]() 的長為______.
的長為______.
(2)以下是小明、小聰的對話:
小明:我加的條件是![]() ,就可以求出
,就可以求出![]() 的長
的長
小聰:你這樣太簡單了,我加的是![]() ,連結
,連結![]() ,就可以證明
,就可以證明![]() 與
與![]() 全等.
全等.
參考上面對話,在屏幕內容中添加條件,編制一道題目(此題目不解答,可以添線、添字母).______.
【答案】3 ![]() ,求
,求![]() 的長
的長
【解析】
(1)連接OC,如圖,利用切線的性質得∠OCD=90°,再根據含30°的直角三角形三邊的關系得到OD=2,然后計算OA+OD即可;
(2)添加∠DCB=30°,求ACAC的長,利用圓周角定理得到∠ACB=90°,再證明∠A=∠DCB=30°,然后根據含30°的直角三角形三邊的關系求AC的長.
解:(1)連接OC,如圖,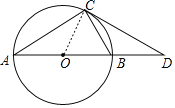
∵CD為切線,
∴OC⊥CD,
∴∠OCD=90°,
∵∠D=30°,
∴OD=2OC=2,
∴AD=AO+OD=1+2=3;
(2)添加∠DCB=30°,求AC的長,
解:∵AB為直徑,
∴∠ACB=90°,
∵∠ACO+∠OCB=90°,∠OCB+∠DCB=90°,
∴∠ACO=∠DCB,
∵∠ACO=∠A,
∴∠A=∠DCB=30°,
在Rt△ACB中,BC= ![]() AB=1,
AB=1,
∴AC= ![]() =
= ![]() .
.
故答案為3;![]() ,求
,求![]() 的長.
的長.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:
【題目】已知平行四邊形![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,且滿足
,且滿足![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .
.
(1)如圖1,若![]() ,
,![]() ,求
,求![]() 的長度;
的長度;
(2)如圖2取![]() 上一點
上一點![]() ,連接
,連接![]() ,在
,在![]() 內取一點
內取一點![]() ,連接
,連接![]() ,
,![]() ,過點
,過點![]() 作
作![]() 的垂線,垂足為點
的垂線,垂足為點![]() ,若
,若![]() ,
,![]() .求證:
.求證:![]() .
.
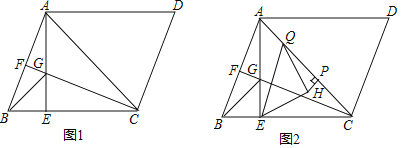
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】蛋黃酥是現下糕點界的網紅,每一顆蛋黃酥金黃誘人的酥皮下都包著一顆細膩綿沙的咸蛋黃,其口口酥心,層層松軟的特點讓人難忘.某商家推出兩款八粒裝的蛋黃酥,其中麻薯豆沙蛋黃酥50元每盒,蓮蓉千層蛋黃酥48元每盒,兩款蛋黃酥非常暢銷,平均每周銷售額為344000元.
(1)受生產能力限制,該商家平時每周生產7000盒八粒裝蛋黃酥,為了保證周銷售額不變,則每周平均需生產麻薯豆沙蛋黃酥多少盒?
(2)在(1)的條件下,為了迎接雙十一大促,該商家提前擴大生產能力,并在雙十一當天,開展蛋黃酥促銷活動,麻薯豆沙蛋黃酥售價降低了![]() a元,其銷量在當天比平時周銷量增加了2000盒,最后當天兩款蛋黃酥的總銷售額比平時周銷售額還多96000元,求a的值.
a元,其銷量在當天比平時周銷量增加了2000盒,最后當天兩款蛋黃酥的總銷售額比平時周銷售額還多96000元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】第二十四屆冬季奧林匹克運動會將于2022年2月4日至2月20日在北京舉行,北京將成為歷史上第一座既舉辦過夏奧會又舉辦過冬奧會的城市.某區舉辦了一次冬奧知識網上答題競賽,甲、乙兩校各有![]() 名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
名學生參加活動,為了解這兩所學校的成績情況,進行了抽樣調查,過程如下,請補充完整.
[收集數據]
從甲、乙兩校各隨機抽取![]() 名學生,在這次競賽中他們的成績如下:
名學生,在這次競賽中他們的成績如下:
甲:![]()
![]()
乙:![]()
![]()
[整理、描述數據]按如下分數段整理、描述這兩組樣本數據:
學校 人數 成績 |
|
|
|
甲 |
|
|
|
乙 |
|
|
|
(說明:優秀成績為![]() ,良好成績為
,良好成績為![]() 合格成績為
合格成績為![]() .)
.)
[分析數據]兩組樣本數據的平均分、中位數、眾數如下表所示:
學校 | 平均分 | 中位數 | 眾數 |
甲 |
|
|
|
乙 |
|
|
|
其中![]() .
.
[得出結論]
(1)小明同學說:“這次競賽我得了![]() 分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
分,在我們學校排名屬中游略偏上!”由表中數據可知小明是 _校的學生;(填“甲”或“乙”)
(2)張老師從乙校隨機抽取--名學生的競賽成績,試估計這名學生的競賽成績為優秀的概率為_ ;
(3)根據以上數據推斷一所你認為競賽成績較好的學校,并說明理由: ;
(至少從兩個不同的角度說明推斷的合理性)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以AB為直徑的⊙O交∠BAD的平分線于點C,交AD于點F,過點C作CD⊥AD于D,交AB的延長線于點E.
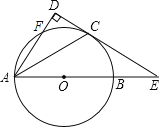
(1)求證:CD為⊙O的切線;
(2)若![]() =
=![]() ,求cos∠DAB的值.
,求cos∠DAB的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于二、四象限內的
的圖象交于二、四象限內的![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() 點,點
點,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的坐標為
的坐標為![]()
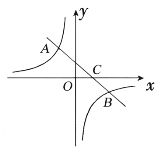
(1)求該反比例函數和一次函數的解析式;
(2)連接![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
(3)設點![]() 在
在![]() 軸上,且滿足
軸上,且滿足![]() 是直角三角形,直接寫出點
是直角三角形,直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
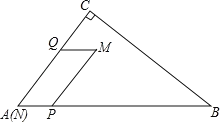
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒1個單位的速度向終點
以每秒1個單位的速度向終點![]() 運動;同時,點
運動;同時,點![]() 從點
從點![]() 出發,沿
出發,沿![]() 以每秒2個單位的速度向終點
以每秒2個單位的速度向終點![]() 運動,當
運動,當![]() 、
、![]() 兩點其中一點到達點
兩點其中一點到達點![]() 時,另一點也隨之停止運動,過點
時,另一點也隨之停止運動,過點![]() 作
作![]() ,過點
,過點![]() 作
作![]() .當點
.當點![]() 與點
與點![]() 不重合時,以
不重合時,以![]() 、
、![]() 為鄰邊作
為鄰邊作![]() .設
.設![]() 、
、![]() 兩點的運動時間為
兩點的運動時間為![]() 秒.
秒.
(1)求線段![]() 的長.(用含
的長.(用含![]() 的代數式表示)
的代數式表示)
(2)點![]() 在邊
在邊![]() 上運動,當點
上運動,當點![]() 落在邊
落在邊![]() 上時,求
上時,求![]() 的值.
的值.
(3)設![]() 與
與![]() 重疊部分圖形的面積為
重疊部分圖形的面積為![]() ,當點
,當點![]() 在
在![]() 內部時,求
內部時,求![]() 與
與![]() 之間的函數關系式.
之間的函數關系式.
(4)當![]() 的一邊是它鄰邊2倍時,直接寫出
的一邊是它鄰邊2倍時,直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,點
,點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 重合),以
重合),以![]() 為腰作等腰直角
為腰作等腰直角![]() ,使
,使![]() ,連接
,連接![]() .
.
(1)觀察猜想
如圖1,當點![]() 在線段
在線段![]() 上時,
上時,
①![]() 與
與![]() 的位置關系為__________;
的位置關系為__________;
②![]() 之間的數量關系為___________(提示:可證
之間的數量關系為___________(提示:可證![]() )
)

(2)數學思考
如圖2,當點![]() 在線段
在線段![]() 的延長線上時,(1)中的①、②結論是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
的延長線上時,(1)中的①、②結論是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明;
(3)拓展延伸
如圖3,當點![]() 在線段
在線段![]() 的延長線時,將
的延長線時,將![]() 沿線段
沿線段![]() 翻折,使點
翻折,使點![]() 與點
與點![]() 重合,連接
重合,連接![]() ,若
,若![]() ,請直接寫出線段
,請直接寫出線段![]() 的長.(提示:做
的長.(提示:做![]() 于
于![]() ,做
,做![]() 于
于![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
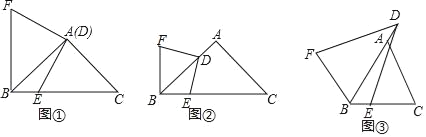
【題目】觀察猜想:(1)如圖①,在Rt△ABC中,∠BAC=90°,AB=AC=3,點D與點A重合,點E在邊BC上,連接DE,將線段DE繞點D順時針旋轉90°得到線段DF,連接BF,BE與BF的位置關系是 ,BE+BF= ;
探究證明:(2)在(1)中,如果將點D沿AB方向移動,使AD=1,其余條件不變,如圖②,判斷BE與BF的位置關系,并求BE+BF的值,請寫出你的理由或計算過程;
拓展延伸:(3)如圖③,在△ABC中,AB=AC,∠BAC=a,點D在邊BA的延長線上,BD=n,連接DE,將線段DE繞著點D順時針旋轉,旋轉角∠EDF=a,連接BF,則BE+BF的值是多少?請用含有n,a的式子直接寫出結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com