
【題目】如圖①,在△ABC中,AB=AC,點D是BC的中點,點E在AD上.
(1)求證:BE=CE.
(2)如圖②,若BE的延長線交AC于點F,且BF⊥AC,垂足為F,AF=BF,原題設其他條件不變.求證:△AEF≌△BCF.
【答案】
(1)證明:∵AB=AC,D是BC的中點,∴∠BAE=∠CAE.
在△ABE和△ACE中, 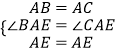 ∴△ABE≌△ACE(SAS).
∴△ABE≌△ACE(SAS).
∴BE=CE 。
(2)證明:∵AB=AC, 點D是BC的中點,
∴AD⊥BC.
∴∠EAF+∠C=90°.
∵BF⊥AC,
∴∠CBF+∠C=90°.
∴∠EAF=∠CBF.
在△AEF和△BCF中, 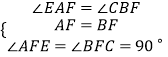
∴△AEF≌△BCF(ASA) 。
【解析】(1)根據等腰三角形的三線合一得出 :∠BAE=∠CAE,然后利用SAS判斷出△ABE≌△ACE , 根據全等三角形對應邊相等得出BE=CE ;
(2)根據等腰三角形的三線合一得出AD⊥BC,根據直角三角形兩銳角互余得出∠EAF+∠C=90° , ∠CBF+∠C=90°,根據同角的余角相等得出∠EAF=∠CBF,然后根據ASA判斷出△AEF≌△BCF 。
【考點精析】解答此題的關鍵在于理解余角和補角的特征的相關知識,掌握互余、互補是指兩個角的數量關系,與兩個角的位置無關,以及對等腰三角形的性質的理解,了解等腰三角形的兩個底角相等(簡稱:等邊對等角).


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:初中數學 來源: 題型:
【題目】小明、小剛和小紅各自隨機選擇本周日的上午或下午去揚州科技館參觀.
(1) 小明、小剛本周日的上午去參觀的概率為_____;
(2) 求他們三人在同一半天去參觀的概率。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△PAB中,PA=PB,M,N,K分別是PA,PB,AB上的點,且AM=BK,BN=AK,若∠MKN=44°,則∠P的度數為( )
A.44°
B.66°
C.88°
D.92°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點B,C,E在y軸上,Rt△ABC經過變換得到Rt△ODE,若點C的坐標為(0,1),AC=2,則這種變換可以是( )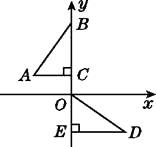
A.△ABC繞點C順時針旋轉90°,再向下平移3個單位長度
B.△ABC繞點C順時針旋轉90°,再向下平移1個單位長度
C.△ABC繞點C逆時針旋轉90°,再向下平移1個單位長度
D.△ABC繞點C逆時針旋轉90°,再向下平移3個單位長度
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線C1:y=x2+4x﹣3與x軸交于A、B兩點,將C1向右平移得到C2,C2與x軸交于B、C兩點.
(1)求拋物線C2的解析式.
(2)點D是拋物線C2在x軸上方的圖象上一點,求S△ABD的最大值.
(3)直線l過點A,且垂直于x軸,直線l沿x軸正方向向右平移的過程中,交C1于點E交C2于點F,當線段EF=5時,求點E的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com