
【題目】如圖,在菱形ABCD中,AB=2,∠BAD=60°,過點D作DE⊥AB于點E,DF⊥BC于點F.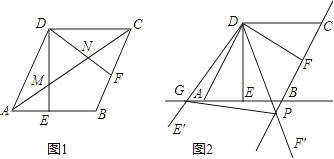
(1)如圖1,連接AC分別交DE、DF于點M、N,求證:MN= ![]() AC;
AC;
(2)如圖2,將△EDF以點D為旋轉中心旋轉,其兩邊DE′、DF′分別與直線AB、BC相交于點G、P,連接GP,當△DGP的面積等于3 ![]() 時,求旋轉角的大小并指明旋轉方向.
時,求旋轉角的大小并指明旋轉方向.
【答案】
(1)
解:證明:如圖1 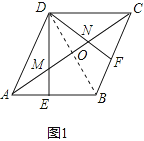 ,
,
連接BD,交AC于O,
在菱形ABCD中,∠BAD=60°,AD=AB,
∴△ABD為等邊三角形,
∵DE⊥AB,
∴AE=EB,
∵AB∥DC,
∴ ![]() =
= ![]() ,
,
同理, ![]() =
= ![]() ,
,
∴MN= ![]() AC;
AC;
(2)
解:解:∵AB∥DC,∠BAD=60°,
∴∠ADC=120°,又∠ADE=∠CDF=30°,
∴∠EDF=60°,
當∠EDF順時針旋轉時,
由旋轉的性質可知,∠EDG=∠FDP,∠GDP=∠EDF=60°,
DE=DF= ![]() ,∠DEG=∠DFP=90°,
,∠DEG=∠DFP=90°,
在△DEG和△DFP中,
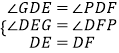 ,
,
∴△DEG≌△DFP,
∴DG=DP,
∴△DGP為等邊三角形,
∴△DGP的面積= ![]() DG2=3
DG2=3 ![]() ,
,
解得,DG=2 ![]() ,
,
則cos∠EDG= ![]() =
= ![]() ,
,
∴∠EDG=60°,
∴當順時針旋轉60°時,△DGP的面積等于3 ![]() ,
,
同理可得,當逆時針旋轉60°時,△DGP的面積也等于3 ![]() ,
,
綜上所述,將△EDF以點D為旋轉中心,順時針或逆時針旋轉60°時,△DGP的面積等于3 ![]() .
.
【解析】(1)連接BD,證明△ABD為等邊三角形,根據等腰三角形的三線合一得到AE=EB,根據相似三角形的性質解答即可;
(2)分∠EDF順時針旋轉和逆時針旋轉兩種情況,根據旋轉變換的性質解答即可.本題考查的是菱形的性質和旋轉變換,掌握旋轉的性質:①對應點到旋轉中心的距離相等;②對應點與旋轉中心所連線段的夾角等于旋轉角;③旋轉前、后的圖形全等是解題的關鍵.


科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,為了測量某建筑物CD的高度,先在地面上用測角儀自A處測得建筑物頂部的仰角是30°,然后在水平地面上向建筑物前進了100m,此時自B處測得建筑物頂部的仰角是45°.已知測角儀的高度是1.5m,請你計算出該建筑物的高度.(取 ![]() =1.732,結果精確到1m)
=1.732,結果精確到1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市在招商引資期間,把已經破產的油泵廠出租給外地某投資商,該投資商為了減少固定資產投資,將原來400平方米的正方形場地建成300平方米的長方形場地,并且長、寬的比為5:3,并且把原來的正方形鐵柵欄圍墻全部利用,圍成新場地的長方形圍墻,請問這些鐵柵欄是否夠用?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=![]() ,AD=10.連接BD,∠DBC的角平分線BE交DC于點E,現把△BCE繞點B逆時針旋轉,記旋轉后的△BCE為△BC′E′.當射線BE′和射線BC′都與線段AD相交時,設交點分別為F,G.若△BFD為等腰三角形,則線段DG長為 .
,AD=10.連接BD,∠DBC的角平分線BE交DC于點E,現把△BCE繞點B逆時針旋轉,記旋轉后的△BCE為△BC′E′.當射線BE′和射線BC′都與線段AD相交時,設交點分別為F,G.若△BFD為等腰三角形,則線段DG長為 .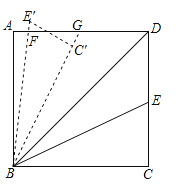
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個古代車輪的碎片,小明為求其外圓半徑,連接外圓上的兩點A、B,并使AB與車輪內圓相切于點D,半徑為OC⊥AB交外圓于點C.測得CD=10cm,AB=60cm,則這個車輪的外圓半徑是( )
A.10cm
B.30cm
C.60cm
D.50cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△AOB中,∠O=90°,AO=8cm,BO=6cm,點C從A點出發,在邊AO上以4cm/s的速度向O點運動,與此同時,點D從點B出發,在邊BO上以3cm/s的速度向O點運動,過OC的中點E作CD的垂線EF,則當點C運動了 s時,以C點為圓心,2cm為半徑的圓與直線EF相切.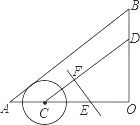
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班為滿足同學們課外活動的需求,要求購排球和足球若干個.已知足球的單價比排球的單價多30元,用500元購得的排球數量與用800元購得的足球數量相等.
(1)排球和足球的單價各是多少元?
(2)若恰好用去1200元,有哪幾種購買方案?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com