
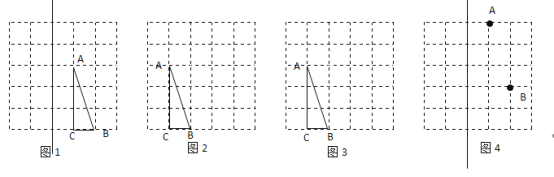
【題目】如圖是由邊長為![]() 的小正方形構成的網格,每個小正方形的頂點叫做格點,
的小正方形構成的網格,每個小正方形的頂點叫做格點,![]() 的頂點在格點.請選擇適當的格點用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
的頂點在格點.請選擇適當的格點用無刻度的直尺在網格中完成下列畫圖,保留連線的痕跡,不要求說明理由.
(1)如圖![]() ,作
,作![]() 關于直線
關于直線![]() 的對稱圖形
的對稱圖形![]() ;
;
(2)如圖![]() ,作
,作![]() 的高
的高![]() ;
;
(3)如圖![]() ,作
,作![]() 的中線
的中線![]() ;
;
(4)如圖![]() ,在直線
,在直線![]() 上作出一條長度為
上作出一條長度為![]() 個單位長度的線段
個單位長度的線段![]() 在
在![]() 的上方
的上方![]() ,使
,使![]() 的值最小.
的值最小.
【答案】(1)圖見解析;(2)圖見解析;(3)圖見解析;(4)圖見解析
【解析】
(1)分別找到A、B、C關于直線l的對稱點![]() ,連接
,連接![]() 、
、![]() 、
、![]() 即可;
即可;
(2)如解圖2,連接CH,交AB于點D,利用SAS證出△ACB≌△CGH,從而得出∠BAC=∠HCG,然后利用等量代換即可求出∠CDB=90°;
(3)如解圖3,連接CP交AB于點E,利用矩形的性質可得AE=BE;
(4)如解圖4,找出點A關于l的對稱點A1,設點A1正下方的格點為C,連接CB,交直線l于點N,設點B正上方的格點為D,連接A1D,交直線l于點M,連接AM,根據平行四邊形的性質和兩點之間線段最短即可推出此時MN即為所求.
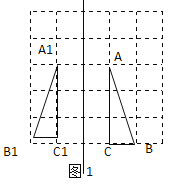
解:(1)分別找到A、B、C關于直線l的對稱點![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,如圖1所示,
,如圖1所示,![]() 即為所求;
即為所求;
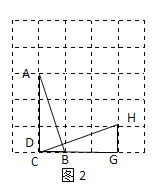
(2)如圖2所示連接CH,交AB于點D,
在△ACB和△CGH中
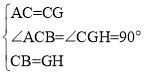
∴△ACB≌△CGH
∴∠BAC=∠HCG
∵∠BAC+∠ABC=90°
∴∠HCG+∠ABC=90°
∴∠CDB=90°
∴CD為△ABC的高,故CD即為所求;
(3)如圖3所示,連接CP交AB于點E
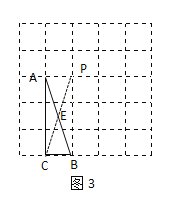
由圖可知:四邊形ACBP為矩形
∴AE=EB
∴CE為△ABC的中線,故CE即為所求;
(4)如圖4所示,找出點A關于l的對稱點A1,設點A1正下方的格點為C,連接CB,交直線l于點N,設點B正上方的格點為D,連接A1D,交直線l于點M,連接AM
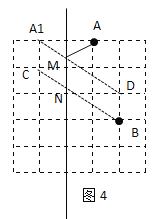
根據對稱性可知:AM=A1M
由圖可知:A1C=BD=1個單位長度,A1C∥BD∥直線l
∴四邊形A1CBD為平行四邊形
∴A1D∥BC
∴四邊形A1CNM和四邊形MNBD均為平行四邊形
∴A1M=CN,MN=BD=1個單位長度
∴AM=CN
∴AM+NB=CN+NB=CB,
根據兩點之間線段最短,此時AM+NB最小,而MN=1個單位長度為固定值,
∴此時![]() 最小,故此時MN即為所求.
最小,故此時MN即為所求.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】先閱讀下列材料,再解答下列問題:
題:分解因式:![]()
解:將“![]() ”看成整體,設
”看成整體,設![]() ,則原式=
,則原式=![]()
![]()
再將“![]() ”還原,得原式=
”還原,得原式=![]() .
.
上述解題用到的是“整體思想”,“整體思想”是數學解題中常用的一種思想方法,請你仿照上面的方法解答下列問題:
(1)因式分解:![]() ;
;![]() .
.
(2)因式分解:![]() ;
;![]() .
.
(3)求證:若![]() 為正整數,則式子
為正整數,則式子![]() 的值一定是某一個正整數的平方.
的值一定是某一個正整數的平方.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方體的長為15,寬為10,高為20,點B離點C的距離為5,一只螞蟻如果要沿著長方體的表面從點A爬到點B,需要爬行的最短距離是__________

查看答案和解析>>
科目:初中數學 來源: 題型:
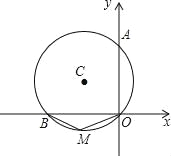
【題目】如圖,⊙C 經過原點且與兩坐標軸分別交于點 A 與點 B,點 B 的坐標為(﹣![]() ,0),M 是圓上一點,∠BMO=120°.⊙C 圓心 C 的坐標是_____.
,0),M 是圓上一點,∠BMO=120°.⊙C 圓心 C 的坐標是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
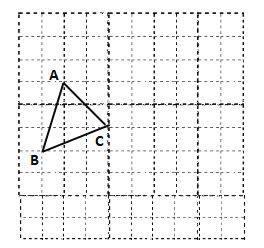
【題目】如圖,在邊長為1的小正方形組成的10×10網絡中(我們把組成網格的小正方形的頂點稱為格點),△ABC的三個頂點分別在網格的格點上
(1)請你在所給的網格中建立平面直角坐標系,使△ABC的頂點A的坐標為(-3,5);
(2)在(1)的坐標系中,直接寫出△ABC其它兩個頂點的坐標;
(3)在(1)的坐標系中,畫出△ABC關于y軸對稱的圖形△A1B1C1 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2﹣4x+c經過點A(2,0).
(1)求拋物線的解析式和頂點坐標;
(2)若點B(m,n)是拋物線上的一動點,點B關于原點的對稱點為C.
①若B、C都在拋物線上,求m的值;
②若點C在第四象限,當AC2的值最小時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
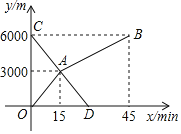
【題目】小玲和弟弟小東分別從家和圖書館同時出發,沿同一條路相向而行,小玲開始跑步,然后改為步行,到達圖書館恰好用45min:小東騎自行車以300m/min的速度直接回家,兩人離家的路程y(m)與各自離開出發地的時間x(min)之間的函數圖象如圖所示.
(1)家與圖書館之間的路程為 m,小東從圖書館到家所用的時間為 .
(2)求小玲步行時y與x之間的函數關系式.
(3)求兩人相遇的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下面材料:
在數學課上,老師提出如下問題:
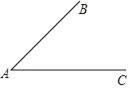
尺規作圖:作已知角的角平分線.
已知:如圖,∠BAC.求作:∠BAC的角平分線AP.
小霞的作法如下:
(1)如圖,在平面內任取一點O;
(2)以點O為圓心,AO為半徑作圓,交射線AB于點D,交射線AC于點E;
(3)連接DE,過點O作射線OP垂直于線段DE,交⊙O于點P;
(4)過點P作射線AP.
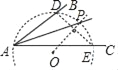
所以射線AP為所求.
老師說:“小霞的作法正確.”
請回答:小霞的作圖依據是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com