【題目】已知關于x、y的方程組
．
（1）當m＝2時，請解關于x、y的方程組；
（2）若關于x、y的方程組中，x為非負數、y為負數，
①試求m的取值范圍；
②當m取何整數時，不等式3mx+2x＞3m+2的解為x＜1．
【答案】（1）
；（2）①﹣2＜m≤
；②m=-1.
【解析】
（1）把m＝2代入方程組，解二元一次方程組，即可解答
（2）①根據x為非負數、y為負數，解出不等式組
②先根據x＜1求出m的值，再把m的值代入不等式即可解答
解：（1）把m＝2代入方程組
中得：
，
①+②得：2x＝10，x＝5，
①﹣②得：﹣2y＝8，y＝﹣4，
∴方程組的解為：；
（2）①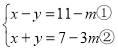
，
①+②得：2x＝18﹣4m，x＝9﹣2m，
①﹣②得：﹣2y＝4+2m，y＝﹣2﹣m，
∵x為非負數、y為負數，
∴
，解得：﹣2＜m≤；
②3mx+2x＞3m+2，
（3m+2）x＞3m+2，
∵不等式3mx+2x＞3m+2的解為x＜1，
∴3m+2＜0，
∴m＜﹣
，
由①得：﹣2＜m≤，
∴﹣2＜m＜﹣，
∵m整數，
∴m＝﹣1；
即當m＝﹣1時，不等式3mx+2x＞3m+2的解為x＜1．
科目：初中數學 來源： 題型：
【題目】如圖，圓E是三角形ABC的外接圓， ∠BAC=45°，AO⊥BC于O，且BO=2，CO=3，分別以BC、AO所在直線建立x軸.
（1）求三角形ABC的外接圓直徑；
（2）求過ABC三點的拋物線的解析式；
（3）設P是（2）中拋物線上的一個動點，且三角形AOP為直角三角形，則這樣的點P有幾個？（只需寫出個數，無需解答過程）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】學習概念：
三角形一邊的延長線與三角形另一邊的夾角叫做三角形的外角．如圖1中∠ACD是△AOC的外角，那么∠ACD與∠A、∠O之間有什么關系呢？
∵∠ACD＝180°﹣∠ACO，∠A+∠O＝180°﹣∠ACO
∴∠ACD＝∠A+ ，
結論：三角形的外角等于與它不相鄰的兩個內角的 ．
問題探究：
(1)如圖2，已知：∠AOB＝∠ACP＝∠BDP＝60°，且AO＝BO，則△AOC △OBD；
(2)如圖3，已知∠ACP＝∠BDP＝45°，且AO＝BO，當∠AOB＝ °，△AOC≌△OBD；
應用結論：
(3)如圖4，∠AOB＝90°，OA＝OB，AC⊥OP，BD⊥OP，請說明：AC＝CD+BD．
拓展應用：
(4)如圖5，四邊形ABCD，AB＝BC，BD平分∠ADC，AE∥CD，∠ABC+∠AEB＝180°，EB＝5，求CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1是一個長為2a、寬為2b的長方形(其中a,b均為正數,且a>b)，沿圖中虛線用剪刀均勻分成四塊相同小長方形，然后按圖2方式拼成一個大正方形。
(1)你認為圖2中大正方形的邊長為___;小正方形(陰影部分)的邊長為___.(用含a、b的代數式表示)
(2)仔細觀察圖2,請你寫出下列三個代數式：(ab)
,(a+b)，ab所表示的圖形面積之間的相等關系，并選取適合a、b的數值加以驗證。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖：在平面直角坐標系中，拋物線
經過A（—2，—4 ），O（0，0），B（2，0）三點.
（1）求拋物線
的解析式和頂點坐標D.
（2）若使
軸上一點P，使P 到A、D的距離之和最小，求P的坐標.
（3）若拋物線對稱軸上一點M，使AM + OM最小，求AM + OM的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1在正方形ABCD中，P是對角線BD上的一點，點E在AD的延長線上，且PA=PE，PE交CD于F.
（1）證明：PC=PE；
（2）求∠CPE的度數；
（3）如圖2，把正方形ABCD改為菱形ABCD，其他條件不變，當∠ABC=120度時，連接CE，試探究線段AP與線段CE的數量關系，并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
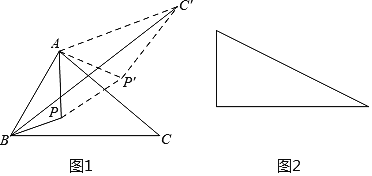
【題目】問題的提出:
如果點P是銳角△ABC內一動點，如何確定一個位置，使點P到△ABC的三頂點的距離之和PA+PB+PC的值為最小?
問題的轉化:
(1)把ΔAPC繞點A逆時針旋轉60度得到
連接
這樣就把確定PA+PB+PC的最小值的問題轉化成確定
的最小值的問題了,請你利用如圖證明:
；
問題的解決:
(2)當點P到銳角△ABC的三項點的距離之和PA+PB+PC的值為最小時，請你用一定的數量關系刻畫此時的點P的位置:_____________________________；
問題的延伸：
(3)如圖是有一個銳角為30°的直角三角形，如果斜邊為2，點P是這個三角形內一動點，請你利用以上方法，求點P到這個三角形各頂點的距離之和的最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】清明時節，張老師和王老師組織八年級
班學生步行到距學校
千米的烈士陵園掃墓．出發時，王老師帶領學生先出發，
分鐘后，張老師騎自行車出發，張老師騎自行車的速度是學生步行速度的
倍，當學生到達烈士陵園時，張老師已經到達個小時，并為大家買好了掃墓門票．
（1）求學生的步行速度和張老師騎自行車的速度各是多少；
（2）當張老師追上學生時，距離烈士陵園還有多遠？
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
