
【題目】某旅行團32人在景區A游玩,他們由成人、少年和兒童組成.已知兒童10人,成人比少年多12人.
(1)求該旅行團中成人與少年分別是多少人?
(2)因時間充裕,該團準備讓成人和少年(至少各1名)帶領10名兒童去另一景區B游玩.景區B的門票價格為100元/張,成人全票,少年8折,兒童6折,一名成人可以免費攜帶一名兒童.
①若由成人8人和少年5人帶隊,則所需門票的總費用是多少元?
②若剩余經費只有1200元可用于購票,在不超額的前提下,最多可以安排成人和少年共多少人帶隊?求所有滿足條件的方案,并指出哪種方案購票費用最少.
【答案】(1)該旅行團中成人17人,少年5人;(2)①1320元,②最多可以安排成人和少年共12人帶隊,有三個方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中當成人10人,少年2人時購票費用最少.
【解析】
(1)設該旅行團中成人![]() 人,少年
人,少年![]() 人,根據兒童10人,成人比少年多12人列出方程組求解即可;
人,根據兒童10人,成人比少年多12人列出方程組求解即可;
(2)①根據一名成人可以免費攜帶一名兒童以及少年8折,兒童6折直接列式計算即可;
②分情況討論,分別求出在a的不同取值范圍內b的最大值,得到符合題意的方案,并計算出所需費用,比較即可.
解:(1)設該旅行團中成人![]() 人,少年
人,少年![]() 人,根據題意,得
人,根據題意,得
![]() ,解得
,解得![]() .
.
答:該旅行團中成人17人,少年5人.
(2)∵①成人8人可免費帶8名兒童,
∴所需門票的總費用為:![]() (元).
(元).
②設可以安排成人![]() 人、少年
人、少年![]() 人帶隊,則
人帶隊,則![]() .
.
當![]() 時,
時,
(ⅰ)當![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() ,此時
,此時![]() ,費用為1160元.
,費用為1160元.
(ⅱ)當![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() ,此時
,此時![]() ,費用為1180元.
,費用為1180元.
(ⅲ)當![]() 時,
時,![]() ,即成人門票至少需要1200元,不合題意,舍去.
,即成人門票至少需要1200元,不合題意,舍去.
當![]() 時,
時,
(ⅰ)當![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() ,此時
,此時![]() ,費用為1200元.
,費用為1200元.
(ⅱ)當![]() 時,
時,![]() ,∴
,∴![]() ,
,
∴![]() ,此時
,此時![]() ,不合題意,舍去.
,不合題意,舍去.
(ⅲ)同理,當![]() 時,
時,![]() ,不合題意,舍去.
,不合題意,舍去.
綜上所述,最多可以安排成人和少年共12人帶隊,有三個方案:成人10人,少年2人;成人11人,少年1人;成人9人,少年3人;其中當成人10人,少年2人時購票費用最少.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
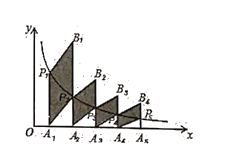
【題目】如圖,分別過反比例函數![]() 圖象上的點
圖象上的點![]() , ...
, ...![]() ···作
···作![]() 軸的垂線,垂足分別為
軸的垂線,垂足分別為![]() ······
······![]() ,連接
,連接![]() ···
···![]() 再以
再以![]() 為一組鄰邊畫一個平行四邊形
為一組鄰邊畫一個平行四邊形![]() ,以
,以![]() 為一組鄰邊畫一個平行四邊形
為一組鄰邊畫一個平行四邊形![]()
![]() ,依此類推,則點
,依此類推,則點![]() 的縱坐標是_____.(結果用含
的縱坐標是_____.(結果用含![]() 代數式表示)
代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣9ax+18a的圖象與x軸交于A,B兩點(A在B的左側),圖象的頂點為C,直線AC交y軸于點D.
(1)連接BD,若∠BDO=∠CAB,求這個二次函數的表達式;
(2)是否存在以原點O為對稱軸的矩形CDEF?若存在,求出這個二次函數的表達式,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
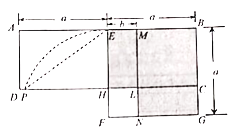
【題目】如圖,在矩形ABCD中,E為AB中點,以BE為邊作正方形BEFG,邊EF交CD于點H,在邊BE上取點M使BM=BC,作MN∥BG交CD于點L,交FG于點N.歐兒里得在《幾何原本》中利用該圖解釋了![]() .現以點F為圓心,FE為半徑作圓弧交線段DH于點P,連結EP,記△EPH的面積為S1,圖中陰影部分的面積為S2.若點A,L,G在同一直線上,則
.現以點F為圓心,FE為半徑作圓弧交線段DH于點P,連結EP,記△EPH的面積為S1,圖中陰影部分的面積為S2.若點A,L,G在同一直線上,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
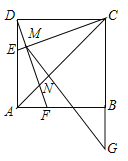
【題目】如圖,正方形![]() ,點
,點![]() 在邊
在邊![]() 上,且
上,且![]() ,
,![]() ,垂足為
,垂足為![]() ,且交
,且交![]() 于點
于點![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,延長
,延長![]() 至
至![]() ,使
,使![]() ,連接
,連接![]() .有如下結論:①
.有如下結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .上述結論中,所有正確結論的序號是( )
.上述結論中,所有正確結論的序號是( )
A. ①②B. ①③C. ①②③D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
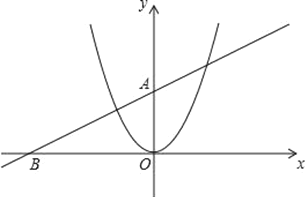
【題目】已知直線y=kx+b經過點A(0,2),B(﹣4,0)和拋物線y=x2.
(1)求直線的解析式;
(2)將拋物線y=x2沿著x軸向右平移,平移后的拋物線對稱軸左側部分與y軸交于點C,對稱軸右側部分拋物線與直線y=kx+b交于點D,連接CD,當CD∥x軸時,求平移后得到的拋物線的解析式;
(3)在(2)的條件下,平移后得到的拋物線的對稱軸與x軸交于點E,P為該拋物線上一動點,過點P作拋物線對稱軸的垂線,垂足為Q,是否存在這樣的點P,使以點E,P,Q為頂點的三角形與△AOB相似?若存在,請求出點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年的3月15日是“國際消費者權益日”,許多家居商城都會利用這個契機進行打折促銷活動.甲賣家的A商品成本為600元,在標價1000元的基礎上打8折銷售.
(1)現在甲賣家欲繼續降價吸引買主,問最多降價多少元,才能使利潤率不低于20%?
(2)據媒體爆料,有一些賣家先提高商品價格后再降價促銷,存在欺詐行為.乙賣家也銷售A商品,其成本、標價與甲賣家一致,以前每周可售出50件,現乙賣家先將標價提高2m%,再大幅降價24m元,使得A商品在3月15日那一天賣出的數量就比原來一周賣出的數量增加了 ![]() m%,這樣一天的利潤達到了20000元,求m的值.
m%,這樣一天的利潤達到了20000元,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知二次函數![]() (
(![]() 為常數,
為常數,![]() )的圖象過點
)的圖象過點![]() 和點
和點![]() ,函數圖象最低點
,函數圖象最低點![]() 的縱坐標為
的縱坐標為![]() .直線
.直線![]() 的解析式為
的解析式為![]()
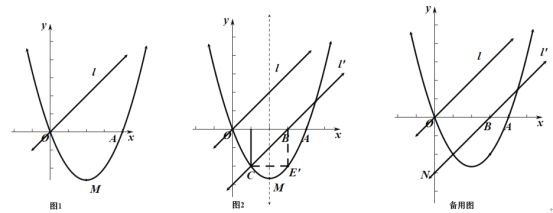
![]() 求二次函數的解析式;
求二次函數的解析式;
![]() 直線
直線![]() 沿
沿![]() 軸向右平移,得直線
軸向右平移,得直線![]() ,
,![]() 與線段
與線段![]() 相交于點
相交于點![]() ,與
,與![]() 軸下方的拋物線相交于點
軸下方的拋物線相交于點![]() ,過點
,過點![]() 作
作![]() 軸于點
軸于點![]() ,把
,把![]() 沿直線
沿直線![]() 折疊,當點
折疊,當點![]() 恰好落在拋物線上點
恰好落在拋物線上點![]() 時(圖
時(圖![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,
的條件下,![]() 與
與![]() 軸交于點
軸交于點![]() ,把
,把![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 得到
得到![]() ,P為
,P為![]() 上的動點,當
上的動點,當![]() 為等腰三角形時,求符合條件的點
為等腰三角形時,求符合條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com