
【題目】數學問題:計算![]() (其中m,n都是正整數,且m≥2,n≥1).
(其中m,n都是正整數,且m≥2,n≥1).
探究問題:為解決上面的數學問題,我們運用數形結合的思想方法,通過不斷地分割一個面積為1的正方形,把數量關系和幾何圖形巧妙地結合起來,并采取一般問題特殊化的策略來進行探究.
探究一:計算![]() .
.
第1次分割,把正方形的面積二等分,其中陰影部分的面積為![]() ;
;
第2次分割,把上次分割圖中空白部分的面積繼續二等分,陰影部分的面積之和為![]() +
+![]() ;
;
第3次分割,把上次分割圖中空白部分的面積繼續二等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后二等分,所有陰影部分的面積之和為![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面積是
,最后空白部分的面積是![]() .
.
根據第n次分割圖可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:計算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面積三等分,其中陰影部分的面積為![]() ;
;
第2次分割,把上次分割圖中空白部分的面積繼續三等分,陰影部分的面積之和為![]() +
+![]() ;
;
第3次分割,把上次分割圖中空白部分的面積繼續三等分,…;
…
第n次分割,把上次分割圖中空白部分的面積最后三等分,所有陰影部分的面積之和為![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面積是
,最后空白部分的面積是![]() .
.
根據第n次分割圖可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
兩邊同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:計算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
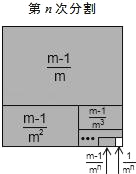
(仿照上述方法,只畫出第n次分割圖,在圖上標注陰影部分面積,并寫出探究過程)

解決問題:計算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需畫出第n次分割圖,在圖上標注陰影部分面積,并完成以下填空)
根據第n次分割圖可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓廣應用:計算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
【答案】![]()
![]()
【解析】
探究三:根據探究二的分割方法依次進行分割,然后表示出陰影部分的面積,再除以3即可;
解決問題:按照探究二的分割方法依次分割,然后表示出陰影部分的面積及,再除以(m-1)即可得解;
拓廣應用:先把每一個分數分成1減去一個分數,然后應用公式進行計算即可得解.
探究三:第1次分割,把正方形的面積四等分,

其中陰影部分的面積為![]() ;
;
第2次分割,把上次分割圖中空白部分的面積繼續四等分,
陰影部分的面積之和為![]() ;
;
第3次分割,把上次分割圖中空白部分的面積繼續四等分,
…,
第n次分割,把上次分割圖中空白部分的面積最后四等分,
所有陰影部分的面積之和為:![]() ,
,
最后的空白部分的面積是![]() ,
,
根據第n次分割圖可得等式:![]() =1﹣
=1﹣![]() ,
,
兩邊同除以3,得![]() =
=![]() ;
;
解決問題:![]() =1﹣
=1﹣![]() ,
,
![]() =
=![]() ;
;
故答案為:![]() =1﹣
=1﹣![]() ,
,![]() ;
;
拓廣應用:![]() ,
,
=1﹣![]() +1﹣
+1﹣![]() +1﹣
+1﹣![]() +…+1﹣
+…+1﹣![]() ,
,
=n﹣(![]() +
+![]() +
+![]() +…+
+…+![]() ),
),
=n﹣(![]() ﹣
﹣![]() ),
),
=n﹣![]() +
+![]() .
.


 口算題卡北京婦女兒童出版社系列答案
口算題卡北京婦女兒童出版社系列答案科目:初中數學 來源: 題型:
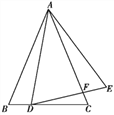
【題目】如圖,在△ABC中,AB=AC,點D在邊BC上,連接AD,將線段AD繞點A逆時針旋轉到AE,使得∠DAE=∠BAC,連接DE交AC于F,請寫出圖中一對相似的三角形:____(只要寫出一對即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小瑩和小亮在筆直的公路上同起點、同終點、同方向勻速步行![]() 米,先到終點的人原地休息.已知小瑩先出發
米,先到終點的人原地休息.已知小瑩先出發![]() 分鐘,在整個步行過程中,兩人的距離
分鐘,在整個步行過程中,兩人的距離![]() (米)與小瑩出發的時間
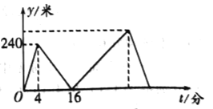
(米)與小瑩出發的時間![]() (分)之間的關系如圖所示,下列結論:①小瑩的步行速度為
(分)之間的關系如圖所示,下列結論:①小瑩的步行速度為![]() 米/分;②小亮用
米/分;②小亮用![]() 分鐘追上小瑩;③小亮走完全程用了
分鐘追上小瑩;③小亮走完全程用了![]() 分鐘;④小亮到達終點時,小瑩離終點還有
分鐘;④小亮到達終點時,小瑩離終點還有![]() 米。其中正確的結論有( )
米。其中正確的結論有( )
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.
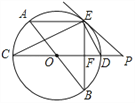
(1)求證:PE是⊙O的切線;
(2)求證:ED平分∠BEP.
查看答案和解析>>
科目:初中數學 來源: 題型:
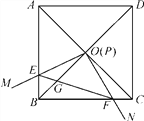
【題目】如圖,邊長為1的正方形ABCD的對角線AC,BD相交于點O,有直角∠MPN,使直角頂點P與點O重合,直角邊PM,PN分別與OA,OB重合,然后逆時針旋轉∠MPN,旋轉角為θ(0°<θ<90°),PM,PN分別交AB,BC于E,F兩點,連接EF交OB于點G,則下列結論:(1)EF=![]() OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=
OE;(2)S四邊形OEBF∶S正方形ABCD=1∶4;(3)BE+BF=![]() OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=
OA;(4)在旋轉過程中,當△BEF與△COF的面積之和最大時,AE=![]() ;(5)OG·BD=AE2+CF2,其中正確的是__.
;(5)OG·BD=AE2+CF2,其中正確的是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲三角形的周長為![]() ,乙三角形的第一條邊長為
,乙三角形的第一條邊長為![]() ,第二條邊長為
,第二條邊長為![]() ,第三條邊比第二條邊短
,第三條邊比第二條邊短![]() .
.
(1)求乙三角形第三條邊的長;
(2)甲三角形和乙三角形的周長哪個大?試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰梯形ABCD中,AD∥BC,E、F是邊BC上的兩點,且BE=CF,DE與AF相交于梯形ABCD內一點O.
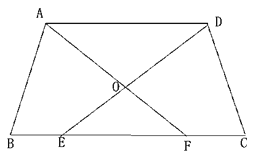
(1)求證:OE=OF;
(2)當EF=AD時,聯結AE、DF,先判斷四邊形AEFD是怎樣的四邊形,再證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦期間某商店進行促銷活動,活動方式有如下兩種:
方式一:每滿200元減50元;
方式二:若標價不超過400元時,打8折;若標價超過400元,則不超過400元的部分打8折,超出400元的部分打6折.
設某一商品的標價為![]() 元:
元:
(1)當![]() 元,按方式二應付多少錢.
元,按方式二應付多少錢.
(2)當![]() 時,
時,![]() 取何值兩種方式的優惠相同.
取何值兩種方式的優惠相同.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com