
【題目】如圖,在邊長為![]() 個單位長度的小正方形組成的網格中,給出了格點
個單位長度的小正方形組成的網格中,給出了格點![]() 和
和![]() (頂點是網格線的交點).點
(頂點是網格線的交點).點![]() 、
、![]() 坐標為
坐標為![]() ,
,![]() .
.
![]() 觀察圖形填空:
觀察圖形填空:![]() 是由
是由![]() 繞________點順時針旋轉________度得到的;
繞________點順時針旋轉________度得到的;
![]() 把
把![]() 中的圖形作為一個新的”基本圖形“,將新的基本圖形繞
中的圖形作為一個新的”基本圖形“,將新的基本圖形繞![]() 點順時針旋轉
點順時針旋轉![]() 度,請作出旋轉后的圖形,其中,
度,請作出旋轉后的圖形,其中,![]() 、
、![]() 、
、![]() 、
、![]() 的對應點分別為
的對應點分別為![]() 、
、![]() 、
、![]() 、
、![]() .依次連接
.依次連接![]() 、
、![]() 、
、![]() 、
、![]() ,則四邊形
,則四邊形![]() 的形狀為________;
的形狀為________;
![]() 以
以![]() 點為位似中心,位似比為
點為位似中心,位似比為![]() (原圖與新圖對應邊的比為
(原圖與新圖對應邊的比為![]() ),作出四邊形
),作出四邊形![]() 的位似圖形.
的位似圖形.

【答案】O,90,正方形
【解析】
(1)由于OB=OB1,OA=OA1,∠AOA1=∠BOB1=90°,則根據旋轉的定義,把△OAB繞O點順時針旋轉90度可得到△OA1B1;
(2)根據關于原點對稱的點的坐標特征寫出A、B、A1、B1的對應點分別為A2、B2、A3、B3的坐標,然后描點即可得到四邊形BB1B2B3,然后根據旋轉的性質得到對角線互相垂直平分且相等可判斷四邊形BB1B2B3為
正方形;
(3)把點B、B1、B2、B3的橫縱坐標都乘以2得到對應點C、D、E、F的坐標,然后描點即可得到四邊形CDEF.
解:(1)△OA1B1是由△OAB繞O點順時針旋轉90度得到的;
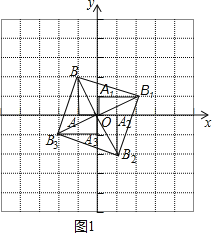
(2)如圖1,四邊形BB1B2B3的為所作,它是正方形;
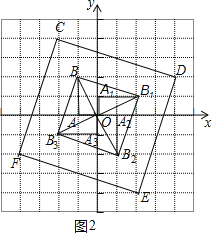
(3)如圖2,四邊形CDEF為所作;
故答案為O,90,正方形.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中有點A(0,0),點A第1次運動到點A1(0,1),第2次運動到點A2(1,0),第3次運動到點A3(1,1),第4次運動到點A4(0,0),第5次運動到點A5(![]() ,1),第6次運動到點A6(
,1),第6次運動到點A6(![]() ,0),第7次運動到點A7(0,1),第8次運動到點A8(0,2),第9次運動到點A9(1,1)…,依次規律運動下去,點A第2019次運動到點A2019的坐標是( )
,0),第7次運動到點A7(0,1),第8次運動到點A8(0,2),第9次運動到點A9(1,1)…,依次規律運動下去,點A第2019次運動到點A2019的坐標是( )
A.(1,288)B.(0,288)C.(1,289)D.(0,289)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖的正方形網格中,每一個小正方形的邊長為1.格點三角形ABC(頂點是網格線交點的三角形)的頂點A、C的坐標分別是(﹣4,6),(﹣1,4).

(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出△ABC關于x軸對稱的△A1B1C1;
(3)△ABC 直角三角形(填“是”或“不是”);
(4)請在y軸上畫一點P,使△PB1C的周長最小,并寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在距樹![]() 米的地面上平放一面鏡子
米的地面上平放一面鏡子![]() ,人退后到距鏡子
,人退后到距鏡子![]() 米的
米的![]() 處,在鏡子里恰巧看見樹頂,若人眼
處,在鏡子里恰巧看見樹頂,若人眼![]() 距地面
距地面![]() 米.
米.

![]() 求樹高;
求樹高;
![]() 和
和![]() 是位似圖形嗎?若是,請指出位似中心;若不是,請說明理由.
是位似圖形嗎?若是,請指出位似中心;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC和∠ACB的平分線相交于點D,過點D作EF∥BC交AB,AC于點E,F,若AB=10,AC=8,則△AEF的周長是_______________。

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=﹣![]() x+
x+![]() 與x軸、y軸分別交于點B、A,與直線y=
與x軸、y軸分別交于點B、A,與直線y=![]() 相交于點C.動點P從O出發在x軸上以每秒5個單位長度的速度向B勻速運動,點Q從C出發在OC上以每秒4個單位長度的速度,向O勻速運動,運動時間為t秒(0<t<2).
相交于點C.動點P從O出發在x軸上以每秒5個單位長度的速度向B勻速運動,點Q從C出發在OC上以每秒4個單位長度的速度,向O勻速運動,運動時間為t秒(0<t<2).
(1)直接寫出點C坐標及OC、BC長;
(2)連接PQ,若△OPQ與△OBC相似,求t的值;
(3)連接CP、BQ,若CP⊥BQ,直接寫出點P坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC是一塊直角三角形紙片,∠ACB=90°,將該三角形紙片折疊,使點A與點C重合,DE為折痕.
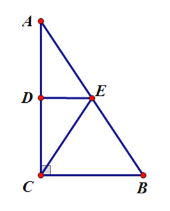
(1)線段AE和BE有怎樣的數量關系?寫出你的結論并進行證明.
結論: .
證明:
(2)直角三角形斜邊的中線和斜邊有怎樣的數量關系?寫出你的結論(不證明).
結論: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC.點D從點B出發沿射線BC移動,以AD為邊在AB的右側作△ADE,且∠DAE=90°,AD=AE.連接CE.
(1)如圖1,若點D在BC邊上,則∠BCE=______度;
(2)如圖2,若點D在BC的延長線上運動.
①∠BCE的度數是否發生變化?請說明理由;
②若BC=6,CD=2,求△ADE的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com