
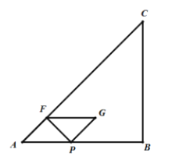
【題目】如圖,在等腰直角![]() 中,
中,![]() 動點
動點![]() 以每秒
以每秒![]() 個單位長度的速度從點
個單位長度的速度從點![]() 向終點
向終點![]() 運動,過點
運動,過點![]() 作
作![]() 于點
于點![]() 以
以![]() 為鄰邊作
為鄰邊作![]() 與等腰直角
與等腰直角![]() 的重疊部分面積為
的重疊部分面積為![]() (平方單位),
(平方單位),![]() ,點
,點![]() 的運動時間為
的運動時間為![]() 秒.
秒.
(1)直接寫出點![]() 落在
落在![]() 邊上時的
邊上時的![]() 值.
值.
(2)求![]() 與
與![]() 的函數關系式
的函數關系式
(3)直接寫出點![]() 分別落在
分別落在![]() 三邊的垂直平分線上時的
三邊的垂直平分線上時的![]() 值
值
【答案】(1)![]() ;(2)
;(2)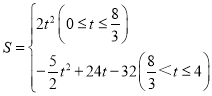 ;(3)
;(3)![]() 或2或4
或2或4
【解析】
(1)畫出圖形,根據題干條件,得出△AFP和△BPG是等腰直角三角形,表示出AP,PB,根據FQ=BG解出t值;
(2)分當點G在BC邊上以及BC左側時,當點G在BC右側時,兩種情況分別求出S和t的關系即可;
(3)分點G在AB、BC、AC的中垂線上求出t值即可.
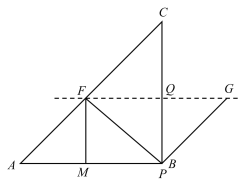
解:(1)當點G落在BC邊上時,如圖,
∵AB=BC=8,∠B=90°,PF⊥AF,
∴在□APGF中,∠AFP=∠FPG=90°,
∴∠A=∠FPA=∠GPB=∠PGB=45°,
即△AFP和△BPG是等腰直角三角形,
∴AP=FG=2t,PB=BG=8-2t,
AP邊上的高FQ=BG=2t,
∴(8-2t)×2=2t,
解得:t=![]() ;
;
(2)當點G在BC邊上以及BC左側時,0≤t≤![]() ,
,
S的值為□APGF的面積,
△APF為等腰直角三角形,
∴△APF中AP邊上的高為t,
則S=2t2,
當點G在BC右側時,![]() <t≤4,
<t≤4,
由題意可得:∠G=45°,∠NMG=90°,FQ=t,
∴△MNG是等腰直角三角形,
∴MN=MG=MB-NB=MB-PB=t-(8-2t)=3t-8,
S=S□APGF -S△MNG=2t×t-![]() (3t-8)2=
(3t-8)2=![]() ,
,
故S和t的函數關系式為: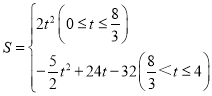 ;
;
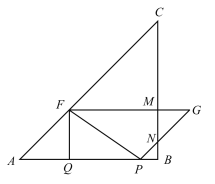
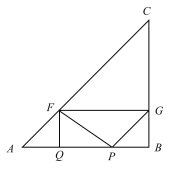
(3)當點G在AB邊的中垂線QH上時,
AH=4,
由題意可得:GH=PH=4-2t,
FM=![]() AP=t,
AP=t,
∴4-2t=t,
解得t=![]() ;
;
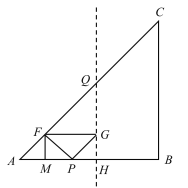
當點G在AC邊的中垂線上時,
可知∠ABQ=45°,
∴△PBG為等腰直角三角形,
∴PB=![]() PG=
PG=![]() AF=AP,
AF=AP,
∴AP=4,
∴t=2;
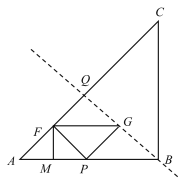
當點G在BC邊中垂線上時,
PQ=FM=![]() AP,
AP,
則此時點P與點B重合,
∴t=4.
綜上所述:點![]() 分別落在
分別落在![]() 三邊的垂直平分線上時,t的值為
三邊的垂直平分線上時,t的值為![]() 或2或4.
或2或4.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某社區購買甲、乙兩種樹苗進行綠化,購買一棵甲種樹苗的價錢比購買一棵乙種樹苗的價錢多 10 元錢,已知購買 20 棵甲種樹苗、30 棵乙種樹苗共需 1 200 元錢.
(1)求購買一棵甲種、一棵乙種樹苗各多少元?
(2)社區決定購買甲、乙兩種樹苗共 400 棵,總費用不超過 10 600 元,那么該社區最多可以購買多少棵甲種樹苗?
查看答案和解析>>
科目:初中數學 來源: 題型:
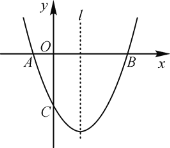
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經過A(-1,0),B(3,0),C(0,-3)三點,直線l是拋物線的對稱軸.
(1)求拋物線的函數解析式;
(2)設點M是直線l上的一個動點,當點M到點A,點C的距離之和最短時,求點M的坐標;
(3)在拋物線上是否存在點N,使S⊿ABN=![]() S⊿ABC,若存在,求出點N的坐標,若不存在,說明理由.
S⊿ABC,若存在,求出點N的坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋中裝有![]() 個分別標有數
個分別標有數![]() 的小球,它們的形狀、大小完全相同,小紅先從口袋里隨機摸出一個小球記下數為
的小球,它們的形狀、大小完全相同,小紅先從口袋里隨機摸出一個小球記下數為![]() ,小穎在剩下的
,小穎在剩下的![]() 個球中隨機摸出一個小球記下數為
個球中隨機摸出一個小球記下數為![]() ,這樣確定了點
,這樣確定了點![]() 的坐標.
的坐標.![]()
(1)請你利用列表法或畫樹狀圖法求點![]() 的橫、縱坐標均能被
的橫、縱坐標均能被![]() 整除的概率.
整除的概率.
(2)記點![]() 關于
關于![]() 軸的對稱點為
軸的對稱點為![]() ,求點
,求點![]() 位于反比例函數
位于反比例函數![]() 圖象上的概率.
圖象上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,菱形ABCD的頂點A的坐標為(3,0),頂點B在y軸正半軸上,頂點D在x軸負半軸上.若拋物線y=-x2-5x+c經過點B、C,則菱形ABCD的面積為_______.
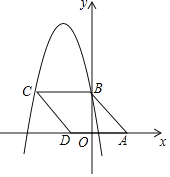
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=x2+bx+c的對稱軸為直線x=1,且經過點(﹣1,0).若關于x的一元二次方程x2+bx+c﹣t=0(t為實數)在﹣1<x<4的范圍內有實數根,則t的取值范圍是________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A(3,4),點B為直線x=﹣2上的動點,點C(x,0)且﹣2<x<3,BC⊥AC垂足為點C,連接AB.若AB與y軸正半軸的所夾銳角為α,當tanα的值最大時x的值為( )

A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地質量監管部門對轄區內的甲、乙兩家企業生產的某同類產品進行檢查,分別隨機抽取了 50 件產品并對某一項關鍵質量指標做檢測,獲得了它們的質量指標值 s ,并對樣本數據(質量指標值 s )進行了整理、描述和分析.下面給出了部分信息.
a.該質量指標值對應的產品等級如下:
質量指標值 | 20 ≤ s 25 | 25 ≤ s 30 | 30 ≤ s 35 | 35 ≤ s 40 | 40 ≤ s ≤ 45 |
等級 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
說明:等級是一等品,二等品為質量合格(其中等級是一等品為質量優秀); 等級是次品為質量不合格.
b.甲企業樣本數據的頻數分布統計表如下(不完整):
c.乙企業樣本數據的頻數分布直方圖如下:
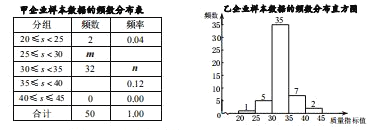
d.兩企業樣本數據的平均數、中位數、眾數、方差如下:
平均數 | 中位數 | 眾數 | 方差 | |
甲企業 | 31.92 | 32.5 | 34 | 11.87 |
乙企業 | 31.92 | 31.5 | 31 | 15.34 |
根據以上信息,回答下列問題:
(1) m 的值為 , n 的值為 ;
(2)若從甲企業生產的產品中任取一件,估計該產品質量合格的概率為 ; 若乙企業生產的某批產品共5 萬件,估計質量優秀的有 萬件;
(3)根據圖表數據,你認為 企業生產的產品質量較好,理由為 .(從某個角度說明推斷的合理性)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com