【題目】將一些數排列成下表中的四列：
第1列 | 第2列 | 第3列 | 第4列 | |
第1行 | 1 | 4 | 5 | 10 |
第2行 | 4 | 8 | 10 | 12 |
第3行 | 9 | 12 | 15 | 14 |
… | … | … | … | … |
（1）第4行第1列的數是多少？直接寫出答案；
（2）第17行的四個數之和是多少？請寫出適當的過程；
（3）數100所在的行和列分別是多少？直接寫出答案.
【答案】(1)16；(2)484；(3) 數100在第10行第1列，第25行第2列，第20行第3列，第46行第4列.
【解析】
（1）觀察可知，第1列的數從上往下依次為
，
，
，
，可得第4行第1列的數；
（2）第1列的數的數為
，第2列的數為
，第3列的數為
，第4列為
，相加即可得到結論；
（3）第3列的數從上往下依次為
，
，
，；第4列的數從上往下依次為，
，
，，根據各列的變化規律可得100所在的行和列．
解：（1）根據表格中的規律，第一列的數分別為1，4，9，…，分別為12，22，32，…，
∴第4行第1列的數是42＝16；
（2）∵第17行第1列的數的數為172，第17行第2列的數為4×17，第17行第3列的數為5×17，第17行第4列為10+2（17﹣1），
∴第17行的四個數之和是172+4×17+5×17+10+2（17﹣1）＝484；
（3）∵100＝102，
∴數100在第10行第1列；
∵100＝4×25，
∴數100在第25行第2列；
∵100＝5×20，
∴數100在第20行第3列；
∵100＝50×2＝（46+4）×2，
∴數100在第46行第4列.
綜上所述，數100在第10行第1列，第25行第2列，第20行第3列，第46行第4列.
名校練考卷期末沖刺卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，∠ABC=∠ACB，AD、BD、CD分別平分△ABC的外角∠EAC、內角∠ABC、外角∠AFC，以下結論：①AD∥BC；②∠ACB=2∠ADB；③∠ADC=90°—∠ABD；④∠BDC=
∠BAC，其中正確的結論有_____________。
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系xOy中，點M的坐標為（x1，y1），點N的坐標為（x2，y2），且x1≠x2，y1≠y2，以MN為邊構造菱形，若該菱形的兩條對角線分別平行于x軸，y軸，則稱該菱形為邊的“坐標菱形”，
（1）已知點A（2，0），B（0，2
），則以AB為邊的“坐標菱形”的面積為 ；
（2）若點C（1，2），點D在直線y＝5上，以CD為邊的“坐標菱形”為正方形，求直線CD解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，四邊形
為正方形，已知點
、
，點
、
在第二象限內.
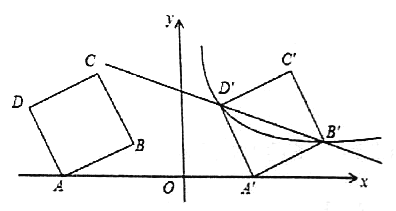
（1）點的坐標___________；
（2）將正方形以每秒
個單位的速度沿
軸向右平移
秒，若存在某一時刻，使在第一象限內點、
兩點的對應點
、
正好落在某反比例函數的圖象上，請求出此時的值以及這個反比例函數的解析式；
（3）在（2）的情況下，問是否存在
軸上的點
和反比例函數圖象上的點
，使得以、、、四個點為頂點的四邊形是平行四邊形？若存在，請直接寫出符合題意的點、的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在正方形
中，連接
，
為射線
上的一個動點（與點
不重合），連接
，的垂直平分線交線段于點
，連接
，
.
提出問題：當點運動時，
的度數是否發生改變？
探究問題：
（1）首先考察點的兩個特殊位置：
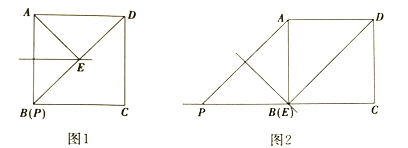
①當點與點
重合時，如圖1所示，
____________
②當
時，如圖2所示，①中的結論是否發生變化？直接寫出你的結論：__________；（填“變化”或“不變化”）
（2）然后考察點的一般位置：依題意補全圖3，圖4，通過觀察、測量，發現：（1）中①的結論在一般情況下_________；（填“成立”或“不成立”）
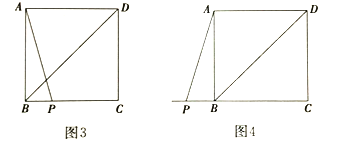
（3）證明猜想：若（1）中①的結論在一般情況下成立，請從圖3和圖4中任選一個進行證明；若不成立，請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
