
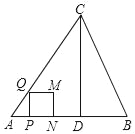
【題目】如圖,在△ABC中,AB=AC=5,AB邊上的高CD=4,點P從點A出發,沿AB以每秒3個單位長度的速度向終點B運動,當點P不與點A、B重合時,過點P作PQ⊥AB,交邊AC或邊BC于點Q,以PQ為邊向右側作正方形PQMN.設正方形PQMN與△ABC重疊部分圖形的面積為S(平方單位),點P運動的時間為t(秒).
(1)直接寫出tanB的值為 .
(2)求點M落在邊BC上時t的值.
(3)當正方形PQMN與△ABC重疊部分為四邊形時,求S與t之間的函數關系式.
(4)邊BC將正方形PQMN的面積分為1:3兩部分時,直接寫出t的值.
【答案】(1)2; (2)![]() ;(3)s=
;(3)s=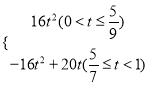 .(4)
.(4)![]() s.
s.
【解析】試題分析:(1)利用三角函數定義求tanB的值.(2) 當點M落在BC邊上時,由題意得:AP=3t,利用tan∠CAB=![]() 求t的值.(3) ①當0<t≤
求t的值.(3) ①當0<t≤![]() 時,如圖1,正方形PQMN與△ABC重疊部分是正方形PQMN,②當N與B重合時,當
時,如圖1,正方形PQMN與△ABC重疊部分是正方形PQMN,②當N與B重合時,當![]() <t<
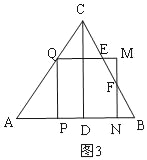
<t<![]() 時,如圖3,正方形PQMN與△ABC重疊部分是五邊形EQPNF,③當
時,如圖3,正方形PQMN與△ABC重疊部分是五邊形EQPNF,③當![]() ≤t<1時,如圖4,正方形PQMN與△ABC重疊部分是梯形EQPB,S與t之間的函數.(4) QG=GM, t=
≤t<1時,如圖4,正方形PQMN與△ABC重疊部分是梯形EQPB,S與t之間的函數.(4) QG=GM, t=![]() s或1s時,邊BC將正方形PQMN的面積分為1:3兩部分.
s或1s時,邊BC將正方形PQMN的面積分為1:3兩部分.
試題解析:
解:(1)∵CD⊥AB,
∴∠ADC=∠ADB=90°,
∵在Rt△ACD中,AD=![]() =3,
=3,
∴BD=AB﹣AD=5﹣3=2,
∴在Rt△BCD中,tan∠B=![]() =
=![]() =2;
=2;
故答案為2.
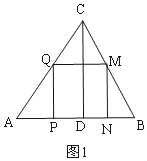
(2)當點M落在BC邊上時,如圖1,
由題意得:AP=3t,
tan∠CAB=![]() ,
,
∴PQ=PN=MN=4t,BN=2t,
∴3t+4t+2t=5,
t=![]() .
.
(3)分三種情況:
①當0<t≤![]() 時,如圖1,正方形PQMN與△ABC重疊部分是正方形PQMN,
時,如圖1,正方形PQMN與△ABC重疊部分是正方形PQMN,
∴S=PQ2=(4t)2=16t2;
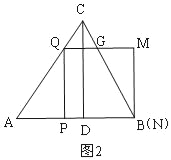
②當N與B重合時,如圖2,
AP=3t,PQ=PB=4t,
∴3t+4t=5,
t=![]() ,
,
當![]() <t<
<t<![]() 時,如圖3,正方形PQMN與△ABC重疊部分是五邊形EQPNF,
時,如圖3,正方形PQMN與△ABC重疊部分是五邊形EQPNF,
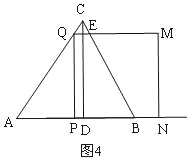
③當![]() ≤t<1時,如圖4,正方形PQMN與△ABC重疊部分是梯形EQPB,
≤t<1時,如圖4,正方形PQMN與△ABC重疊部分是梯形EQPB,
∴AP=3t,PN=4t,
∴BN=7t﹣5,PB=4t﹣(7t﹣5)=﹣3t+5,
在Rt△APQ中,AQ=5t,
∴QC=5﹣5t,
∵AC=AB,
∴∠ACB=∠ABC,
∵QE∥AB,
∴∠QEC=∠ABC,
∴∠QEC=∠ACB,
∴QE=QC=5﹣5t,
∴S=S梯形QPBE=![]() (QE+PB)×PQ,
(QE+PB)×PQ,
=![]() (5﹣5t+5﹣3t)×4t=﹣16t2+20t;
(5﹣5t+5﹣3t)×4t=﹣16t2+20t;
綜上所述,S與t之間的函數關系式為:
S=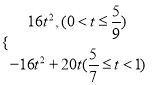 .
.
(4)如圖2,當t=![]() 時,CQ=QG=5﹣5t=
時,CQ=QG=5﹣5t=![]() ,
,
∴GM=4t﹣![]() =
=![]() ,
,
∴QG=GM,
∴S△QGB=S△GMB,
∴S梯形GQPB:S△GMB=3:1,
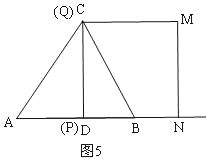
當P與D重合時,t=1,如圖5,
則S△CDB:S四邊形CBNM=![]() ×2×4:(42﹣
×2×4:(42﹣![]() ×2×4),
×2×4),
=1:3,
綜上所述,t=![]() s或1s時,邊BC將正方形PQMN的面積分為1:3兩部分.
s或1s時,邊BC將正方形PQMN的面積分為1:3兩部分.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
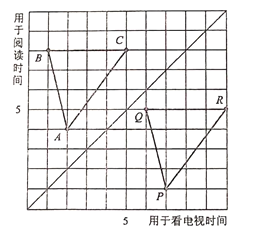
【題目】圖中,點A,B,C,P,Q,R顯示了6名學生平均每周用于閱讀課外書的時間和用于看電視的時間(單位:h)
(1)用有序數對表示圖中點A,B,C,P,Q,R
(2)圖中方格紙的對角線的左上方的點有什么共同的特點?它右下方的點呢?
(3)三角形ABC的圖形經過怎樣的變換后得到三角形PQR的圖形?其中點A對應點P,點B對應點Q,點C對應點R
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明根據學習函數的經驗,對函數![]() 的圖像與性質進行了探究.請補充完整:
的圖像與性質進行了探究.請補充完整:
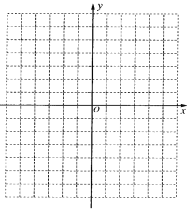
(1)先填表,再在如圖所示的平面直角坐標系中,描全表中各對對應值為坐標的點,并畫出該函數的圖像:
x | … | -5 | -4 | -3 | -2 | 0 | 1 | 2 | 3 | … |
| … | 2 |
| 3 | -3 |
| 0 | … |
(2)結合函數的圖像,說出兩條不同類型的性質;
①________________________________;____________________________________.
②![]() 的圖像是由
的圖像是由![]() 的圖像如何平移得到?
的圖像如何平移得到?
___________________________________________.
(3)當函數值![]() 時,x的取值范圍是____________span>.
時,x的取值范圍是____________span>.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,每一個小方格的邊個長為1個單位.

(1)請寫出△ABC各點的坐標;
(2)若把△ABC向上平移2個單位,再向右平移2個單位得到△A1B1C1,在圖中畫出△A1B1C1;
(3)求△A1B1C1的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
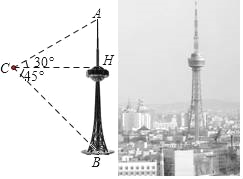
【題目】吉林省廣播電視塔(簡稱“吉塔”)是我省目前最高的人工建筑,也是俯瞰長春市美景的最佳去處.某科技興趣小組利用無人機搭載測量儀器測量“吉塔”的高度.已知如圖將無人機置于距離“吉塔”水平距離138米的點C處,則從無人機上觀測塔尖的仰角恰為30°,觀測塔基座中心點的俯角恰為45°.求“吉塔”的高度.(注: ![]() ≈1.73,結果保留整數)
≈1.73,結果保留整數)
查看答案和解析>>
科目:初中數學 來源: 題型:
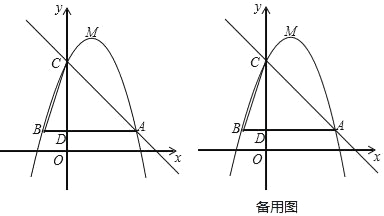
【題目】如圖,已知二次函數y=﹣x2+bx+c(其中b,c為常數)的圖象經過點A(3,1),點C(0,4),頂點為點M,過點A作AB∥x軸,交y軸于點D,交該二次函數圖象于點B,連結BC.
(1)求該二次函數的解析式及點M的坐標.
(2)若將該二次函數圖象向下平移m(m>0)個單位,使平移后得到的二次函數圖象的頂點落在△ABC的內部(不包括△ABC的邊界),求m的取值范圍.
(3)沿直線AC方向平移該二次函數圖象,使得CM與平移前的CB相等,求平移后點M的坐標.
(4)點P是直線AC上的動點,過點P作直線AC的垂線PQ,記點M關于直線PQ的對稱點為M′.當以點P、A、M、M′為頂點的四邊形為平行四邊形時,直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在正方形ABCD中,F是CD邊上一點(不與C、D重合),過點D作DG⊥BF交BF延長線于點G.連接AG,交BD于點E,交CD于點M,連接EF.若DG=4,AG=![]() ,則EF的長為____________.
,則EF的長為____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知方程:x![]() ﹣2x﹣8=0,解決一下問題:
﹣2x﹣8=0,解決一下問題:
(1)不解方程判斷此方程的根的情況;
(2)請按要求分別解這個方程:①配方法;②因式分解法.
(3)這些方法都是將解 轉化為解 ;
(4)嘗試解方程:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com