【題目】如圖，已知
的斜邊
，
．
以點
為圓心作圓，當半徑為多長時，直線
與
相切？為什么？
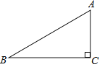
以點為圓心，分別以
和
為半徑作兩個圓，這兩個圓與直線分別有怎樣的位置關系？
【答案】（1）以點
為圓心，當半徑為
時，
與
相切；（2）以點為圓心，分別以
和
為半徑作兩個圓，這兩個圓與直線分別相離和相交.
【解析】
（1）過點C作CD垂直于AB，根據直線與圓相切時，圓心到直線的距離等于圓的半徑，可得出圓C與AB相切時，CD為此時圓C的半徑，在直角三角形ABC中，由AB及AC的長，利用勾股定理求出BC的長，由直角三角形的面積可以由斜邊AB與高CD乘積的一半來，也可以由兩直角邊乘積的一半來求，可得出CD的長，即為AB與圓C相切時的半徑；
（2）用半徑和CD的長比較后即可得到結論．
解：
過作
，交于點
，如圖所示：
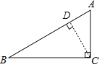
的斜邊
，
，
根據勾股定理得：
，
∵
，
∴
，
則以點為圓心，當半徑為時，與相切；
∵
∴以點為圓心，分別以和為半徑作兩個圓，這兩個圓與直線分別相離和相交；
科目：初中數學 來源： 題型：
【題目】如圖，已知一次函數y＝kx+k+1的圖象與一次函數y＝﹣x+4的圖象交于點A（1，a）．
（1）求a、k的值；
（2）根據圖象，寫出不等式﹣x+4＞kx+k+1的解；
（3）結合圖形，當x＞2時，求一次函數y＝﹣x+4函數值y的取值范圍；
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小賢與小杰在探究某類二次函數問題時，經歷了如下過程：
求解體驗
(1)已知拋物線
經過點(-1,0),則
= ，頂點坐標為 ，該拋物線關于點(0,1）成中心對稱的拋物線的表達式是 .
抽象感悟
我們定義：對于拋物線
,以
軸上的點
為中心，作該拋物線關于
點
對稱的拋物線
,則我們又稱拋物線為拋物線的“衍生拋物線”，點為“衍生中心”.
(2)已知拋物線
關于點
的衍生拋物線為，若這兩條拋物線有交點，求
的取值范圍.
問題解決
(3) 已知拋物線
①若拋物線的衍生拋物線為
,兩拋物線有兩個交點，且恰好是它們的頂點，求
的值及衍生中心的坐標；
②若拋物線關于點
的衍生拋物線為
,其頂點為
；關于點
的衍生拋物線為
，其頂點為
；…；關于點
的衍生拋物線為
，其頂點為
；…(
為
正整數).求
的長(用含的式子表示).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】風電已成為我國繼煤電、水電之后的第三大電源，風電機組主要由塔桿和葉片組成（如圖①），圖②是平面圖．光明中學的數學興趣小組針對風電塔桿進行了測量，甲同學站在平地上的A處測得塔桿頂端C的仰角是55°，乙同學站在巖石B處測得葉片的最高位置D的仰角是45°（D，C，H在同一直線上，G，A，H在同一條直線上），他們事先從相關部門了解到葉片的長度為15米（塔桿與葉片連接處的長度忽略不計），巖石高BG為4米，兩處的水平距離AG為23米，BG⊥GH，CH⊥AH，求塔桿CH的高．（參考數據：tan55°≈1.4，tan35°≈0.7，sin55°≈0.8，sin35°≈0.6）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著人們“節能環保，綠色出行”意識的增強，越來越多的人喜歡騎自行車出行，同時也給自行車商家帶來商機. 某自行車行銷售
型，
型兩種自行車，經統計，2019年此車行銷售這兩種自行車情況如下：自行車銷售總額為8萬元. 每輛型自行車的售價比每輛型自行車的售價少200元，型自行車銷售數量是自行車的1. 25倍， 自行車銷售總額比A型自行車銷售總額多
.
（1）求每輛型自行車的售價多少元.
（2）若每輛型自行車進價1400元，每輛型自行車進價1300元，求此自行車行2019年銷售
型自行車的總利潤.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】二次函數
，
，
是常數，且
中的
與
的部分對應值如下表所示，則下列結論中，正確的個數有（ ）
|
|
|
|
|
|
|
|
|
|
；
當
時，
；
當
時，的值隨值的增大而減小；
方程
有兩個不相等的實數根．
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，有長為24m的籬笆，圍成中間隔有一道籬笆的長方形的花圃，且花圃的長可借用一段墻體(墻體的最大可用長度a＝10m)．
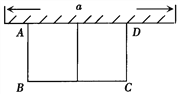
(1)如果所圍成的花圃的面積為45m2，試求寬AB的長；
(2)按題目的設計要求，能圍成面積比45m2更大的花圃嗎?如果能，請求出最大面積，并說明圍法；如果不能，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
