
【題目】完成下列各題:
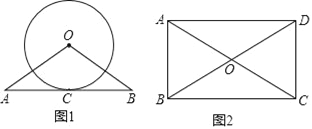
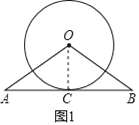
(1)如圖,已知直線AB與⊙O相切于點C,且AC=BC,求證:OA=OB.
(2)如圖,矩形ABCD的兩條對角線相交于點O,∠AOD=120°,AB=3,求AC的長.
【答案】(1)證明見解析;(2)6cm
【解析】試題分析:(1)根據(jù)線段垂直平分線的性質:線段垂直平分線上的點到兩端點的距離相等來證明;
(2)根據(jù)矩形性質得出AC=BD,OA=OB,求出∠AOB=60°,得出△AOB是等邊三角形,求出∠ADB=30°,得出AC=BD=2AB=6cm即可.
(1)證明:連接OC,
∵直線AB與⊙O相切于點C,
∴OC⊥AB,
又∵AC=BC,
∴OC垂直平分AB,
∴OA=OB;
(2)證明:∵四邊形ABCD是矩形,
∴AC=BD,OA=OC=![]() AC,BO=DO=
AC,BO=DO=![]() BD,∠BAD=90°,
BD,∠BAD=90°,
∴OA=OB,
∵∠AOD=120°,
∴∠AOB=60°,
∴△AOB是等邊三角形,
∴∠ABO=60°,∠ADB=30°,
∴AC=BD=2AB=6cm.


科目:初中數(shù)學 來源: 題型:
【題目】2017年度中央機關及其直屬機構公務員招考網(wǎng)上報名已經(jīng)結束,據(jù)初步統(tǒng)計,網(wǎng)上報名人數(shù)約有211.5萬人,數(shù)據(jù)211.5萬用科學記數(shù)法可表示為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀理解:
【問題情境】金老師給“數(shù)學小達人”小明和小軍提出這樣一個問題:
如圖1,△ABC中,∠B=2∠C,AD是∠BAC的平分線.求證:AB+BD=AC.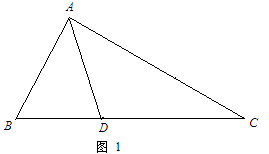
【證明思路】小明的證明思路是:如圖2,在AC上截取AE=AB,連接DE.……
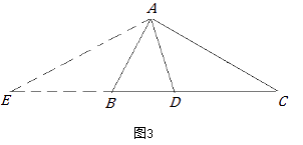
小軍的證明思路是:如圖3,延長CB至點E,使BE=AB,連接AE.可以證得:AE=DE.……
(1)請你從他們的思路中,任意選擇一種思路繼續(xù)完成下一步的證明.
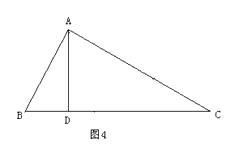
(2)【變式探究】如圖4,金老師把“AD是∠BAC的平分線”改成“AD是BC邊上的高”,其它條件不變,那么AB+BD=AC還成立嗎?若成立,請證明;若不成立,寫出正確結論,并說明理由.
(3)【遷移拓展】如圖5,△ABC中,∠B=2∠C.求證:AC2—AB2=AB×BC.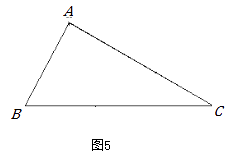
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】商店某天銷售了14件襯衫,其領口尺寸統(tǒng)計如表:
領口尺寸(單位:cm) | 38 | 39 | 40 | 41 | 42 |
件數(shù) | 1 | 5 | 3 | 3 | 2 |
則這14件襯衫領口尺寸的眾數(shù)與中位數(shù)分別是( )
A.39cm、39cm
B.39cm、39.5cm
C.39cm、40cm
D.40cm、40cm
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】為了解某校九年級學生的身高情況,隨機抽取部分學生的身高進行調查,利用所得數(shù)據(jù)繪成如圖統(tǒng)計圖表:
頻數(shù)分布表
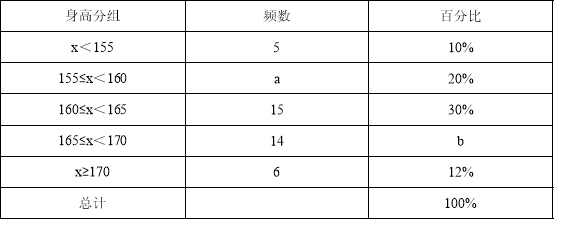
(1)填空:a= ,b= ;
(2)補全頻數(shù)分布直方圖;
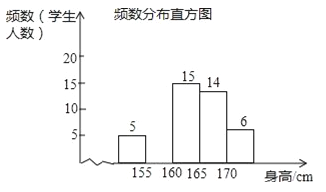
(3)該校九年級共有600名學生,估計身高不低于165cm的學生大約有多少人?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖是二次函數(shù)![]() 圖像的一部分,其對稱軸為x=-l,且過點(-3,0).下列說法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),
圖像的一部分,其對稱軸為x=-l,且過點(-3,0).下列說法:①abc<0;②2a-b=O;③4a+2b+c<0;④若(-5,y1),![]() 是拋物線上兩點,則y1>y2,其中說法正確的有( )
是拋物線上兩點,則y1>y2,其中說法正確的有( )
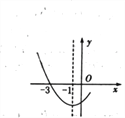
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】對60個數(shù)據(jù)進行處理時,適當分組,各組數(shù)據(jù)個數(shù)之和與百分率之和分別等于( )
A.60,1
B.60,60
C.1,60
D.1,1
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
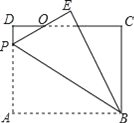
【題目】如圖,矩形ABCD中,AB=8,BC=6,P為AD上一點,將△ABP沿BP翻折至△EBP,PE與CD相交于點O,BE與CD相交于點G,且OE=OD,則AP的長為______.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com