
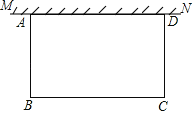
【題目】如圖,在足夠大的空地上有一段長為a(a≥50)米的舊墻MN,某人利用舊墻和木欄圍成一個矩形菜園ABCD,其中AD≤MN,已知矩形菜園的一邊靠墻,另三邊一共用了100米木欄.
(1)若圍成的矩形菜園的面積為450平方米,求所利用舊墻AD的長;
(2)求矩形菜園ABCD面積的最大值.
【答案】(1)AD的長為90m或者10m;(2)矩形菜園面積S的最大值為1250m2.
【解析】
(1)設AB=xm,則BC=(100﹣2x)m,由矩形面積公式可得x(100﹣2x)=450,解之即可解答:
(2)設AD=bm,利用矩形面積公式得矩形菜園面積S=![]() ,配方得
,配方得![]() ,根據二次函數的性質即可求得S的最大值.
,根據二次函數的性質即可求得S的最大值.
(1)設AB=xm,則BC=(100﹣2x)m,
根據題意得x(100﹣2x)=450,解得x1=5,x2=45,
當x=5時,100﹣2x=90,
當x=45時,100﹣2x=10;
答:AD的長為90m或10m;
(2)設AD=bm,
∴矩形菜園面積![]()
∵a≥50,
則b=50時,S有最大值,最大值為1250m2.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案科目:初中數學 來源: 題型:
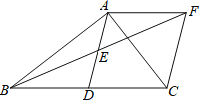
【題目】如圖,在![]() ABC中,AD是BC邊上的中線,點E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.
ABC中,AD是BC邊上的中線,點E是AD的中點,過點A作AF∥BC交BE的延長線于F,連接CF.
(1)求證:![]() AEF≌△DEB;
AEF≌△DEB;
(2)若∠BAC=90°,求證:四邊形ADCF是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,已知∠ACB=90°,AC=BC=4,若點E在△ABC內部運動,且滿足AE2=BE2+2CE2,則點E的運動路徑長是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖反映了我國2014-2019年快遞業務量(位:億件)及年增長率(%)的情況
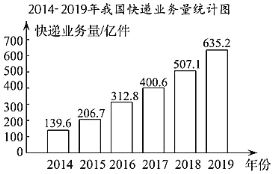
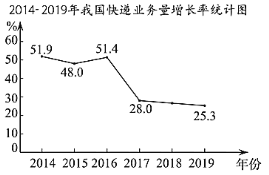
(以上數據來源于國家統計局網站)
根據統計圖提供的信息,下列推斷不合理的是( )
A.2014-2019年,我國快遞業務量的年平均值超過300億件
B.與2017年相比,2018年我國快遞業務量的增長率超過25%
C.2014-2019年,我國快遞業務量與年增長率都是逐年增長
D.2019年我國的快遞業務量比2014年的4倍還多
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 是邊
是邊![]() 上的一點(不與點
上的一點(不與點![]() 重合),邊
重合),邊![]() 上點
上點![]() 在點
在點![]() 的右邊且
的右邊且![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
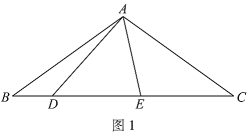
(1)如圖1,
①依題意補全圖1;
②求證:![]() ;
;
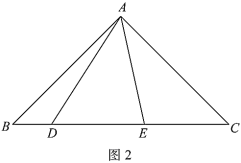
(2)如圖2,![]() ,用等式表示線段
,用等式表示線段![]() ,
,![]() ,
,![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,在圖中按下列步驟進行尺規作圖:
,在圖中按下列步驟進行尺規作圖:
① | 以 |
② | 分別以 |
③ | 畫射線 |
下列說法錯誤的是( )
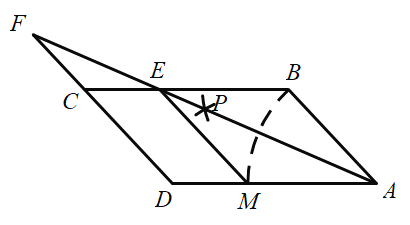
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,則
,則![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家經營打印耗材的門店經銷各種打印耗材,其中某一品牌硒鼓的進價為![]() 元/個,售價為
元/個,售價為![]() 元/個(
元/個(![]() ).下面是門店在銷售一段時間后銷售情況的反饋:
).下面是門店在銷售一段時間后銷售情況的反饋:
①若每個硒鼓按定價30元的8折出售,可獲![]() 的利潤;
的利潤;
②如果硒鼓按30元/個的價格出售,每月可售出500個,在此基礎上,售價每增加5元,月銷售量就減少50個.
(1)求![]() 的值,并寫出該品牌硒鼓每月的銷售量
的值,并寫出該品牌硒鼓每月的銷售量![]() (個)與售價
(個)與售價![]() (元/個)之間的函數關系式,并注明自變量
(元/個)之間的函數關系式,并注明自變量![]() 的取值范圍;
的取值范圍;
(2)求該耗材店銷售這種硒鼓每月獲得的利潤![]() (元)與售價
(元)與售價![]() (元/個)之間的函數關系式,并求每月獲得的最大利潤;
(元/個)之間的函數關系式,并求每月獲得的最大利潤;
(3)在新冠肺炎流行期間,這種硒鼓的進價降低為![]() 元/個,售價為
元/個,售價為![]() 元/個(
元/個(![]() ).耗材店在2月份仍然按照銷售量與售價關系不變的方式銷售,并決定將當月銷售這種硒鼓獲得的利潤全部捐贈給火神山醫院,支援武漢抗擊新冠肺炎.若要使這個月銷售這種硒鼓獲得的利潤
).耗材店在2月份仍然按照銷售量與售價關系不變的方式銷售,并決定將當月銷售這種硒鼓獲得的利潤全部捐贈給火神山醫院,支援武漢抗擊新冠肺炎.若要使這個月銷售這種硒鼓獲得的利潤![]() (元)隨售價
(元)隨售價![]() (元/個)的增大而增大,請直接寫出
(元/個)的增大而增大,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() (
(![]() 是常數,
是常數,![]() )與
)與![]() 軸交于
軸交于![]() 兩點,頂點
兩點,頂點![]() 給出下列結論:①
給出下列結論:①![]() ;②若
;②若![]() 在拋物線上,則
在拋物線上,則![]() ;③關于
;③關于![]() 的方程
的方程![]() 有實數解,則
有實數解,則![]() ;④當
;④當![]() 時,
時,![]() 為等腰直角三角形,其中正確的結論是( )
為等腰直角三角形,其中正確的結論是( )
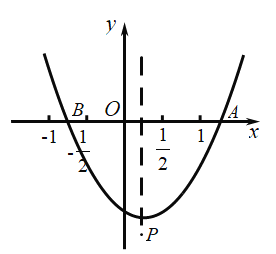
A.①②B.①③C.②③D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com