
【題目】如圖,在平行四邊形ABCD中,E為BC的中點,連接AE并延長交DC的延長線于點F.
(1)求證:AB=CF;
(2)當BC與AF滿足什么數量關系時,四邊形ABFC是矩形,并說明理由.

【答案】(1)見解析;(2)當BC=AF時,四邊形ABFC是矩形,理由見解析
【解析】
(1)根據平行四邊形的性質得到兩角一邊對應相等,利用AAS判定△ABE≌△FCE,從而得到AB=CF;
(2)由已知可得四邊形ABFC是平行四邊形,BC=AF,根據對角線相等的平行四邊形是矩形,可得到四邊形ABFC是矩形.
(1)證明:∵四邊形ABCD是平行四邊形
∴AB∥CD,AB=CD
∴![]() ,
, ![]()
∵E為BC的中點
∴BE=EC
∴ △ABE≌△FCE
∴ AB=CF.
(2)解:當BC=AF時,四邊形ABFC是矩形.理由如下:
∵AB∥CF,AB=CF
∴四邊形ABFC是平行四邊形
∵BC=AF
∴四邊形ABFC是矩形.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
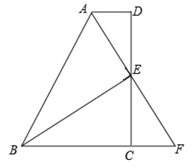
【題目】如圖,在四邊形 ABCD 中,AD∥BC,E 為 CD 的中點,連接 AE、BE,延長 AE 交 BC 的 延長線于點 F.
(1)△DAE 和△CFE 全等嗎?說明理由;
(2)若 AB=BC+AD,說明 BE⊥AF;
(3)在(2)的條件下,若 EF=6,CE=5,∠D=90°,你能否求出 E 到 AB 的距離?如果能 請直接寫出結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點![]() 為平面直角坐標系的原點,在矩形
為平面直角坐標系的原點,在矩形![]() 中,兩邊
中,兩邊![]() 、
、![]() 分別在
分別在![]() 軸和
軸和![]() 軸上,且點
軸上,且點![]() 滿足:
滿足:![]() .
.


(1)求點![]() 的坐標(___,_____);
的坐標(___,_____);
(2)若過點![]() 的直線
的直線![]() 與矩形
與矩形![]() 的
的![]() 邊交于點
邊交于點![]() ,且將矩形
,且將矩形![]() 的面積分為
的面積分為![]() 兩部分,
兩部分,
①求直線![]() 的解析式;
的解析式;
②在直線![]() 確定一點
確定一點![]() ,使得
,使得![]() 的面積等于矩形
的面積等于矩形![]() 的面積,求點
的面積,求點![]() 的坐標;
的坐標;
(3)![]() 在線段
在線段![]() 上,
上,![]() ,
,![]() 在坐標軸上,
在坐標軸上,![]() 為(2)中直線
為(2)中直線![]() 上一動點,若四點
上一動點,若四點![]() 、
、![]() 、
、![]() 、
、![]() 構成平行四邊形,直接寫出
構成平行四邊形,直接寫出![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩人中選拔一人參加射擊比賽,現對他們的射擊成績進行了測試,5次打靶命中的環數如下:
甲:8,7,9,8,8; 乙:9,6,10,8,7;
(1)將下表填寫完整:
平均數 | 中位數 | 方差 | |
甲 | 8 | ||
乙 | 8 | 2 |
(2)根據以上信息,若你是教練,你會選擇誰參加射擊比賽,理由是什么?
(3)若乙再射擊一次,命中8環,則乙這六次射擊成績的方差會 .(填“變大”或“變小”或“不變”)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一個正整數能表示為兩個連續偶數的平方差,那么稱這個正整數為“奇巧數”,如12=![]() ,20=
,20=![]() ,28=
,28=![]() ,……,因此12,20,28這三個數都是奇巧數。
,……,因此12,20,28這三個數都是奇巧數。
(1)52,72都是奇巧數嗎?為什么?
(2)設兩個連續偶數為2n,2n+2(其中n為正整數),由這兩個連續偶數構造的奇巧數是8的倍數嗎?為什么?
(3)研究發現:任意兩個連續“奇巧數”之差是同一個數,請給出驗證。
查看答案和解析>>
科目:初中數學 來源: 題型:
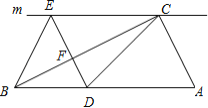
【題目】如圖,在![]() 中,
中,![]() ,過點
,過點![]() 的直線
的直線![]() ,
,![]() 為
為![]() 邊上一點,過點
邊上一點,過點![]() 作
作![]() 交直線
交直線![]() 于點
于點![]() ,垂足為點
,垂足為點![]() ,連結
,連結![]() 、
、![]() .
.
(1)求證:![]() ;
;
(2)當點![]() 是
是![]() 中點時,四邊形
中點時,四邊形![]() 是什么特殊四邊形?說明你的理由;
是什么特殊四邊形?說明你的理由;
(3)若點![]() 是
是![]() 中點,當四邊形
中點,當四邊形![]() 是正方形時,則
是正方形時,則![]() 大小滿足什么條件?
大小滿足什么條件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某山是某市民周末休閑爬山的好去處,但總有些市民隨手丟垃圾的情況出現.為了美化環境,提高市民的環保意識,某外國語學校某附屬學校青年志愿者協會組織50人的青年志愿者團隊,在周末前往臨某森林公園撿垃圾.已知平均每分鐘男生可以撿3件垃圾,女生可以撿2件垃圾,且該團隊平均每分鐘可以撿130件垃圾.請問該團隊的男生和女生各多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為4,點G、H分別是BC、CD邊上的點,直線GH與AB、AD的延長線相交于點E、F,連接AG、AH.
(1)當BG=2,DH=3時,則GH:HF= ,∠AGH= °;
(2)若BG=3,DH=1,求DF、EG的長;
(3)設BG=x,DH=y,若△ABG∽△FDH,求y與x之間的函數關系式,并求出y的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,AB⊥x軸,垂足為A.反比例函數y=![]() (x>0)的圖象經過點C,交AB于點D.已知AB=4,BC=
(x>0)的圖象經過點C,交AB于點D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)連接OC,若BD=BC,求OC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com