2015年是中國人民抗日戰爭暨世界反法西斯勝利70周年，9月3日全國各地將舉行有關紀念活動.為了解初中學生對二戰歷史的知曉情況，某初中課外興趣小組在本校學生中開展了專題調查活動，隨機抽取了部分學生進行問卷調查，根據學生答題情況，將結果分為A、B、C、D四類，其中A類表示“非常了解”、B類表示“比較了解”、C類表示“基本了解”、D類表示“不太了解”，調查的數據經整理后形成下列尚未完成的條形統計圖（如圖①）和扇形統計圖（如圖②）：
（1）在這次抽樣調查中，一共抽查了 名學生；
（2）請把圖①中的條形統計圖補充完整；
（3）圖②的扇形統計圖中D類部分所對應扇形的圓心角的度數為 °；
（4）如果這所學校共有初中學生1500名，請你估算該校初中學生中對二戰歷史“非常了解”和“比較了解”的學生共有多少名？
互動課堂系列答案
激活思維智能訓練課時導學練系列答案科目：初中數學 來源： 題型：
如圖，把△EFP按圖所示的方式放置在菱形ABCD中，使得頂點E、F、P分別在線段AB、AD、AC上.已知EP=FP=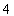
，EF=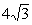
，∠BAD=60°，且AB
.（1）求∠EPF的大小；
（2）若AP=6，求AE+AF的值；
（3）若△EFP的三個頂點E、F、P分別在線段AB、AD、AC上運動，請直接寫出AP長的最大值和最小值.
查看答案和解析>>
科目：初中數學 來源： 題型：
小明在課外學習時遇到這樣一個問題：
定義：如果二次函數y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常數）與y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常數）滿足a1+a2=0，b1=b2，c1+c2=0，則稱這兩個函數互為“旋轉函數”．
求函數y=﹣x2+3x﹣2的“旋轉函數”．
小明是這樣思考的：由函數y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根據a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能確定這個函數的“旋轉函數”．
請參考小明的方法解決下面問題：
（1）寫出函數y=﹣x2+3x﹣2的“旋轉函數”；
（2）若函數y=﹣x2+
mx﹣2與y=x2﹣2nx+n互為“旋轉函數”，求（m+n）2015的值；
（3）已知函數y=﹣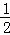
（x+1）（x﹣4）的圖象與x軸交于點A、B兩點，與y軸交于點C，點A、B、C關于原點的對稱點分布是A1，B1，C1，試證明經過點A1，B1，C1的二次函數與函數y=﹣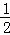（x+1）（x﹣4）互為“旋轉函數．”
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
.
在正方形
的邊
上，若
的面積為
則線段
的長為 ．