
���}Ŀ��ͨ�^�W(xu��)��(x��)�^��ֵ,�҂�֪��![]() �Ď����x�ǔ�(sh��)�S�ϱ�ʾ��(sh��)
�Ď����x�ǔ�(sh��)�S�ϱ�ʾ��(sh��)![]() �ڔ�(sh��)�S�ϵČ���(y��ng)�c(di��n)�cԭ�c(di��n)�ľ��x,�磺
�ڔ�(sh��)�S�ϵČ���(y��ng)�c(di��n)�cԭ�c(di��n)�ľ��x,�磺![]() ��ʾ
��ʾ![]() �ڔ�(sh��)�S�ϵČ���(y��ng)�c(di��n)��ԭ�c(di��n)�ľ��x.
�ڔ�(sh��)�S�ϵČ���(y��ng)�c(di��n)��ԭ�c(di��n)�ľ��x.![]() ,��
,��![]() ��ʾ
��ʾ![]() ��
��![]() �ڔ�(sh��)�S�ό���(y��ng)�ă��c(di��n)֮�g�ľ��x,��Ƶ�,
�ڔ�(sh��)�S�ό���(y��ng)�ă��c(di��n)֮�g�ľ��x,��Ƶ�,![]() ����
����![]() ��ʾ
��ʾ![]() ��
��![]() �ڔ�(sh��)�S�ό���(y��ng)�ă��c(di��n)֮�g�ľ��x��һ��أ��c(di��n)
�ڔ�(sh��)�S�ό���(y��ng)�ă��c(di��n)֮�g�ľ��x��һ��أ��c(di��n)![]() ��
��![]() �ڔ�(sh��)�S�Ϸքe��ʾ��(sh��)
�ڔ�(sh��)�S�Ϸքe��ʾ��(sh��)![]() ��
��![]() ����ô
����ô![]() ��
��![]() ֮�g�ľ��x�ɱ�ʾ��
֮�g�ľ��x�ɱ�ʾ��![]() .
.
Ո����(j��)�^��ֵ�Ď����x���Y(ji��)�ϔ�(sh��)�S������І��}��
��1����(sh��)�S�ϱ�ʾ![]() ��
��![]() �ă��c(di��n)֮�g�ľ��x��___����(sh��)�S��
�ă��c(di��n)֮�g�ľ��x��___����(sh��)�S��![]() ��
��![]() ���c(di��n)�ľ��x��
���c(di��n)�ľ��x��![]() ���c(di��n)
���c(di��n)![]() ��ʾ�Ĕ�(sh��)��
��ʾ�Ĕ�(sh��)��![]() ���t�c(di��n)
���t�c(di��n)![]() ��ʾ�Ĕ�(sh��)��___.
��ʾ�Ĕ�(sh��)��___.
��2���c(di��n)![]() ��
��![]() ��
��![]() �ڔ�(sh��)�S�Ϸքe��ʾ��(sh��)
�ڔ�(sh��)�S�Ϸքe��ʾ��(sh��)![]() ��
��![]() ��
��![]() ,��ô
,��ô![]() ���c(di��n)
���c(di��n)![]() .�c(di��n)
.�c(di��n)![]() �ľ��x֮�Ϳɱ�ʾ��_ (�ú��^��ֵ��ʽ�ӱ�ʾ)����
�ľ��x֮�Ϳɱ�ʾ��_ (�ú��^��ֵ��ʽ�ӱ�ʾ)����![]() ���c(di��n)
���c(di��n)![]() .�c(di��n)
.�c(di��n)![]() �ľ��x֮������Сֵ���t
�ľ��x֮������Сֵ���t![]() ��ȡֵ������_ __.
��ȡֵ������_ __.
��3��![]() ����Сֵ��_ __.
����Сֵ��_ __.
���𰸡���1��2��1��7����2��|x+1|+|x-2|��-1��x��2����3��3
��������
��1������(j��)��(sh��)�S��A��B���c(di��n)֮�g�ľ��x|AB|=|a-b|�����딵(sh��)ֵ�\(y��n)�ý^��ֵ������������c(di��n)�g�ľ��x��
��2������(j��)��(sh��)�S�σ��c(di��n)֮�g�ľ��x��ʽ����A��B�ľ��x�cA��C�ľ��x֮�ͣ��M��|x-3|+|x+2|=7��x��ֵ�������N����ӑՓ���D(zhu��n)���鷽�̽�Q���}��
��3����(d��ng)1��x��4�r(sh��)��|x-1|+|x-4|����Сֵ��|4-1|=3��
�⣺��1����(sh��)�S�ϱ�ʾ2��4�ă��c(di��n)֮�g�ľ��x��4-2=2��
��(sh��)�S��P��Q���c(di��n)�ľ��x��3���c(di��n)P��ʾ�Ĕ�(sh��)��4���t�c(di��n)Q��ʾ�Ĕ�(sh��)��4-3=1��4+3=7��
��2��A��B�ľ��x�cA��C�ľ��x֮�ͣ��ɱ�ʾ��|x+1|+|x-2|��
��|x-3|+|x+2|=7����(d��ng)x��-1�r(sh��)��|x+1|+|x-2|=2-x-x-1=1-2x�o��Сֵ��
��(d��ng)-1��x��2�r(sh��)��|x+1|+|x-2|=x+1+2-x=3��
��(d��ng)x��2�r(sh��)��x+1+x-2=2x-1��3��
����A���c(di��n)B���c(di��n)C�ľ��x֮������Сֵ���tx��ȡֵ������-1��x��2��
��3��ԭʽ=|x-1|+|x-4|��
��(d��ng)1��x��4�r(sh��)��|x-1|+|x-4|����Сֵ��|4-1|=3
�ʴ𰸞飺��1��2��1��7����2��|x+1|+|x-2|��-1��x��2����3��3



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
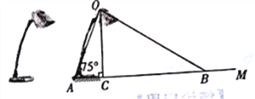
���}Ŀ���D�������ˮƽ�����ϵ��_����ƽ��ʾ��D������sʽ����AO�L��40 cm,�cˮƽ�����γɵĊA�ǡ�OAM���75��(���ܟ�����s��Ӱ�).�ɹ�Դ0����Ĺ⾀��?z��)����γɹ⾀OC��OB���cˮƽ�����γɵĊA�ǡ�OCA,��OBA�քe��90���30��.
(1)��ԓ�_����������Č���BC.(�����]�������أ��Y(ji��)�����_��1 cm��������(sh��)��(j��):sin75���0.97,cos75���0.26�� ![]() ��1.73)
��1.73)
(2)�������������L��60 cm,���{(di��o)�����ֵĽǶȣ��ܷ��_����������85 cm�Č���?
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ������܇˾�C(j��)С��ij��������\(y��n)�I����һ�l�|������Ĵ���ϡ����Ҏ(gu��)����|���������@��������г�ӛ����£�����λ��ǧ�ף�
+15��-3��+14��-11��+10��-18��+14
��1�������һ���˿��͵�Ŀ�ĵؕr(sh��)��С���x�����܇�c(di��n)�ľ��x�Ƕ��٣�
��2���x�_������l(f��)�c(di��n)���h(yu��n)�r(sh��)�Ƕ���ǧ�ף�
��3������܇�ĺ�������0.06��/ǧ�ף��̓r(ji��)��4.5Ԫ/�����@�����繲��֧���������X��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����֪ƽ����߅��![]() �����L
�����L![]() ��
��![]() ��ʹ
��ʹ![]() ���B��
���B��![]() �c
�c![]() ����
����![]() �c(di��n).
�c(di��n).
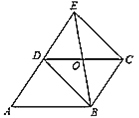
(1)���C��![]() ��
��
(2)��(d��ng)![]() �r(sh��)���B�m(x��)
�r(sh��)���B�m(x��)![]() ��
��![]() �����C����߅��
�����C����߅��![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��С��Ԫ����(ji��)�������6�c(di��n)�^߀�]��7�c(di��n)���������������A�^(q��)SM�V��ȥ�I�|�����x�ҕr(sh��)���l(f��)�F(xi��n)���ҵĕr(sh��)��ϕr(sh��)��c��ᘄ����غϣ����x�ҵĕr(sh��)�g��_______(�Î��c(di��n)�֎����ʾ��ע��������������).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ�����ڳ��Д�(sh��)�W(xu��)�W(xu��)��(x��)�Пo̎�����ڔ�(sh��)�W(xu��)���(d��ng)�n�ϣ����ώ�Ҫ��ͬ�W(xu��)�������W(xu��)֪�R�����ßo�̶ȵ�ֱ�ߺ͈AҎ(gu��)�Д�����֪��AOB���Dz���ֱ�ǣ��ס��҃���ͬ�W(xu��)���Խo����ͬ�����������Д��AOB�Dz���ֱ��
�ף���D1����OA��OB�Ϸքeȡ�c(di��n)CD����C��A�ģ�CD�L��돽��������OB�ķ������L�����c(di��n)E����OE��OD���t��AOB��90����
�ң���D2����OA��OB�Ϸքe��ȡOM��4��(g��)��λ�L�ȣ�ON��3��(g��)��λ�L�ȣ���MN��5��(g��)��λ�L�ȣ��t��AOB��90����
�ס��҃�λͬ�W(xu��)�������_���ǣ�������
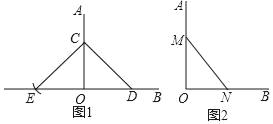
A. �����_���Ҳ����_B. �����_���ײ����_
C. ���Ҷ������_D. ���Ҷ����_
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪������ABCD�У���B��60��������60���ǵ�ֱ�����ǰ��60���ǵ���c(di��n)�ŵ�����ABCD����c(di��n)A̎����߅�քe�c���ε�߅BC��CD�����c(di��n)F��E.
(1)(��D1)���C��AE=AF��
(2)�B�Y(ji��)EF����AC���c(di��n)H(��D2)��ԇ̽��AB��AF��AH֮�g���P(gu��n)ϵ��
(3)��AB��6��EF��2![]() ����CE��DE����FH���L.
����CE��DE����FH���L.


�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
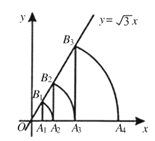
���}Ŀ����D����ֱ֪��y��![]() x���c(di��n)A1������(bi��o)��(1��0)���^�c(di��n)A1��x�S�Ĵ�����ֱ�����c(di��n)B1����ԭ�c(di��n)O��A�ģ�OB1���L��돽������x�S���c(di��n)A2�����^�c(di��n)A2��x�S�Ĵ�����ֱ�����c(di��n)B2����ԭ�c(di��n)O��A�ģ�OB2���L��돽������x�S���c(di��n)A3���������������M(j��n)����ȥ���t�c(di��n)A6������(bi��o)��____________��
x���c(di��n)A1������(bi��o)��(1��0)���^�c(di��n)A1��x�S�Ĵ�����ֱ�����c(di��n)B1����ԭ�c(di��n)O��A�ģ�OB1���L��돽������x�S���c(di��n)A2�����^�c(di��n)A2��x�S�Ĵ�����ֱ�����c(di��n)B2����ԭ�c(di��n)O��A�ģ�OB2���L��돽������x�S���c(di��n)A3���������������M(j��n)����ȥ���t�c(di��n)A6������(bi��o)��____________��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D��ֱ��AB��x�S���c(di��n)B��2��0������y�S���c(di��n)A��0��2����ֱ��DM��x�S�����S���c(di��n)M��������AB���c(di��n)C��DM=3���B��DA����DAC=90����
��1����ֱ��AB�Ľ���ʽ��
��2����D�c(di��n)����(bi��o)���^O��D��B���c(di��n)�Ē��タ����ʽ��
��3�����c(di��n)P�Ǿ���OB�ϵĄ�(d��ng)�c(di��n)���^�c(di��n)P��x�S�Ĵ�����AB��F������2���В��タ��E���BCE���Ƿ����Pʹ��BPF�c��FCE���ƣ������ڣ�Ո���P�c(di��n)����(bi��o)�����������f�����ɣ�

�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com