
【題目】某研究性學習小組在探究矩形的折紙問題時,將一塊直角三角板的直角頂點繞著矩形ABCD(AB<BC)的對角線交點O旋轉(如圖①→②→③),圖中M、N分別為直角三角板的直角邊與矩形ABCD的邊CD、BC的交點.
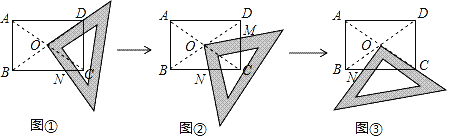
(1)該學習小組中一名成員意外地發現:在圖①(三角板的一直角邊與OD重合)中,BN2=CD2+CN2;在圖③(三角板的一直角邊與OC重合)中,CN2=BN2+CD2.請你對這名成員在圖①和圖③中發現的結論選擇其一說明理由.
(2)試探究圖②中BN、CN、CM、DM這四條線段之間的關系,寫出你的結論,并說明理由.
【答案】(1)見解析;(2)見解析.
【解析】
(1)連接DN,根據矩形得出OB=OD,根據線段垂直平分線得出BN=DN,根據勾股定理求出DN的平方,即可求出答案;
(2)延長NO交AD于點P,連接PM,MN,證△BNO≌△DPO,推出OP=ON,DP=BN,根據線段垂直平分線求出PM=MN,根據勾股定理求出即可.
(1)選①.證明如下:連接DN,
∵四邊形ABCD是矩形,∴OB=OD,
∵∠DON=90°,∴BN=DN,
∵∠BCD=90°,∴DN2=CD2+CN2,∴BN2=CD2+CN2;
(2)延長NO交AD于點P,連接PM,MN,
∵四邊形ABCD是矩形,∴OD=OB,AD∥BC,∴∠DPO=∠BNO,∠PDO=∠NBO,
在△BON和△DOP中,∵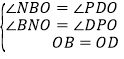 ,∴△BON≌△DOP(AAS),∴ON=OP,BN=PD,
,∴△BON≌△DOP(AAS),∴ON=OP,BN=PD,
∵∠MON=90°,∴PM=MN,
∵∠ADC=∠BCD=90°,∴PM2=PD2+DM2,MN2=CM2+CN2,∴PD2+DM2=CM2+CN2,∴BN2+DM2=CM2+CN2.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線AB經過⊙O上的點C,直線AO與⊙O交于點E和點D,OB與⊙O交于點F,連接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.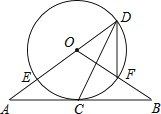
(1)求證:①直線AB是⊙O的切線;②∠FDC=∠EDC;
(2)求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強學生的交通安全意識,某中學和交警大隊聯合舉行了“我當一日小交警”活動,星期天選派部分學生到交通路口值勤,協助交通警察維護交通秩序.若每一個路口安排4人,那么還剩下78人;若每個路口安排8人,那么最后一個路口不足8人,但不少于4人.求這個中學共選派值勤學生多少人?共有多少個交通路口安排值勤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,航空母艦始終以40千米/時的速度由西向東航行,飛機以800千米/時的速度從艦上起飛,向西航行執行任務,如果飛機在空中最多能連續飛行4個小時,那么它在起飛_____小時后就必須返航,才能安全停在艦上?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為9,將正方形折疊,使頂點D落在BC邊上的點E處,折痕為GH.若BE:EC=2:1,則線段CH的長是( )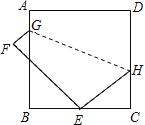
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AB=AC,把△ABC繞A點沿順時針方向旋轉得到△ADE,連接BD,CE交于點F.
(1)求證:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,當四邊形ADFC是菱形時,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小東根據學習一次函數的經驗,對函數y=|2x﹣1|的圖象和性質進行了探究.下面是小東的探究過程,請補充完成:
(1)函數y=|2x﹣1|的自變量x的取值范圍是 ;
(2)已知:
①當x=![]() 時,y=|2x﹣1|=0;
時,y=|2x﹣1|=0;
②當x>![]() 時,y=|2x﹣1|=2x﹣1
時,y=|2x﹣1|=2x﹣1
③當x<![]() 時,y=|2x﹣1|=1﹣2x;
時,y=|2x﹣1|=1﹣2x;
顯然,②和③均為某個一次函數的一部分.
(3)由(2)的分析,取5個點可畫出此函數的圖象,請你幫小東確定下表中第5個點的坐標(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐標系xOy中,作出函數y=|2x﹣1|的圖象;
(5)根據函數的圖象,寫出函數y=|2x﹣1|的一條性質.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是工人師傅用同一種材料制成的金屬框架,已知![]() ,
,![]() ,
,![]() ,其中
,其中![]() 的周長為24cm,
的周長為24cm,![]() ,則制成整個金屬框架所需這種材料的總長度為( )
,則制成整個金屬框架所需這種材料的總長度為( )

A. 45cm B. 48cm C. 51cm D. 54cm
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
①0是絕對值最小的有理數;②相反數大于本身的數是負數;③數軸上原點兩側的數互為相反數;![]() 是有理數.
是有理數.
A. ①② B. ①③ C. ①②③ D. ②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com