
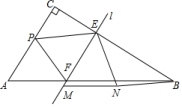
【題目】如圖,Rt![]() ABC中,∠C=90°,AC=10,BC=16.動點P以每秒3個單位的速度從點A開始向點C移動,直線l從與AC重合的位置開始,以相同的速度沿CB方向平行移動,且分別與CB,AB邊交于E,F兩點,點P與直線l同時出發(fā),設(shè)運動的時間為t秒,當(dāng)點P移動到與點C重合時,點P和直線l同時停止運動.在移動過程中,將
ABC中,∠C=90°,AC=10,BC=16.動點P以每秒3個單位的速度從點A開始向點C移動,直線l從與AC重合的位置開始,以相同的速度沿CB方向平行移動,且分別與CB,AB邊交于E,F兩點,點P與直線l同時出發(fā),設(shè)運動的時間為t秒,當(dāng)點P移動到與點C重合時,點P和直線l同時停止運動.在移動過程中,將![]() PEF繞點E逆時針旋轉(zhuǎn),使得點P的對應(yīng)點M落在直線l上,點F的對應(yīng)點記為點N,連接BN,當(dāng)BN∥PE時,t的值為_____.
PEF繞點E逆時針旋轉(zhuǎn),使得點P的對應(yīng)點M落在直線l上,點F的對應(yīng)點記為點N,連接BN,當(dāng)BN∥PE時,t的值為_____.
【答案】![]()
【解析】
作NH⊥BC于H.首先證明∠PEC=∠NEB=∠NBE,推出EH=BH,根據(jù)cos∠PEC=cos∠NEB,推出![]() =
=![]() ,由此構(gòu)建方程解決問題即可.
,由此構(gòu)建方程解決問題即可.
解:作NH⊥BC于H.
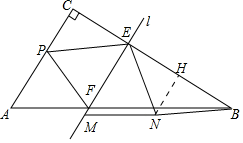
∵EF⊥BC,∠PEF=∠NEF,
∴∠FEC=∠FEB=90°,
∵∠PEC+∠PEF=90°,∠NEB+∠FEN=90°,
∴∠PEC=∠NEB,
∵PE∥BN,
∴∠PEC=∠NBE,
∴∠NEB=∠NBE,
∴NE=NB,
∵HN⊥BE,
∴EH=BH,
∴cos∠PEC=cos∠NEB,
∴![]() =
=![]() ,
,
∵EF∥AC,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EF=EN=![]() (16﹣3t),
(16﹣3t),
∴![]() =
= ,
,
整理得:63t2﹣960t+1600=0,
解得t=![]() 或
或![]() (舍棄),
(舍棄),
故答案為:![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】某學(xué)校組織健康知識競賽,每班參加競賽的人數(shù)相同,成績?yōu)?/span>![]() ,
,![]() ,
,![]() ,
,![]() 四個等級,其中相應(yīng)等級的得分依次記為100分,90分,80分,70分,其中100分和90分為優(yōu)秀.學(xué)校將八年級一班和二班的成績整理并繪制成如下的統(tǒng)計圖與統(tǒng)計表.
四個等級,其中相應(yīng)等級的得分依次記為100分,90分,80分,70分,其中100分和90分為優(yōu)秀.學(xué)校將八年級一班和二班的成績整理并繪制成如下的統(tǒng)計圖與統(tǒng)計表.
一班競賽成績統(tǒng)計圖
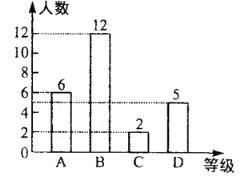
二班競賽成績統(tǒng)計圖
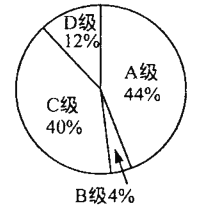
一班和二班競賽成績統(tǒng)計表(部分空缺)
成績 班級 | 眾數(shù) | 中位數(shù) | 優(yōu)秀率 | 平均分 |
一班 | 90 |
|
| 87.6 |
二班 |
| 80 |
|
|
請根據(jù)以上圖表的信息解答下列問題:
(1)求![]() ,
,![]() ,
,![]() 的值.
的值.
(2)若全校共有750名學(xué)生參加競賽,估計成績優(yōu)秀的學(xué)生有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,邊長為2的正方形ABCD的頂點A在y軸上,頂點D在反比例函數(shù)y=(x>0)的圖像上,已知點B的坐標(biāo)是(![]() ,
,![]() ),則k的值為( )
),則k的值為( )
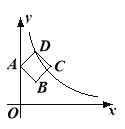
A.10 B.8 C.6 D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 與反比例函數(shù)
與反比例函數(shù)![]() 的圖象交于A(m,6),B(3,n)兩點.
的圖象交于A(m,6),B(3,n)兩點.
(1)求一次函數(shù)的解析式;
(2)求![]() 的面積;
的面積;
(3)根據(jù)圖象直接寫出![]() 的x的取值范圍
的x的取值范圍

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
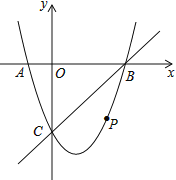
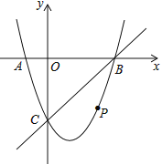
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 、
、![]() 兩點,
兩點,![]() 點在原點的左側(cè),
點在原點的左側(cè),![]() 點的坐標(biāo)為(
點的坐標(biāo)為(![]() ,
,![]() ),與
),與![]() 軸交于
軸交于![]() (
(![]() ,
,![]() ),點
),點![]() 是直線
是直線![]() 下方的拋物線上一動點.
下方的拋物線上一動點.
(1)求這個二次函數(shù)的表達(dá)式.
(2)連結(jié)![]() 、
、![]() ,并把△
,并把△![]() 沿
沿![]() 邊翻折,得到四邊形
邊翻折,得到四邊形![]() , 那么是否存在點
, 那么是否存在點![]() ,使四邊形
,使四邊形![]() 為菱形?若存在,請求出此時點
為菱形?若存在,請求出此時點![]() 的坐標(biāo);若不存在,請說明理由.
的坐標(biāo);若不存在,請說明理由.
(3)當(dāng)點![]() 運動到什么位置時,四邊形
運動到什么位置時,四邊形![]() 的面積最大并求出此時
的面積最大并求出此時![]() 點的坐標(biāo)和四邊形
點的坐標(biāo)和四邊形![]() 的最大面積.
的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】實行垃圾分類和垃圾資源化利用,關(guān)系廣大人民群眾生活環(huán)境,關(guān)系節(jié)約使用資源,也是社會文明水平的一個重要體現(xiàn).某環(huán)保公司研發(fā)了甲、乙兩種智能設(shè)備,可利用最新技術(shù)將干垃圾進(jìn)行分選破碎制成固化成型燃料棒,干垃圾由此變身新型清潔燃料.某垃圾處理廠從環(huán)保公司購入以上兩種智能設(shè)備若干,已知購買甲型智能設(shè)備花費![]() 萬元,購買乙型智能設(shè)備花費
萬元,購買乙型智能設(shè)備花費![]() 萬元,購買的兩種設(shè)備數(shù)量相同,且兩種智能設(shè)備的單價和為
萬元,購買的兩種設(shè)備數(shù)量相同,且兩種智能設(shè)備的單價和為![]() 萬元.
萬元.
![]() 求甲、乙兩種智能設(shè)備單價;
求甲、乙兩種智能設(shè)備單價;
![]() 垃圾處理廠利用智能設(shè)備生產(chǎn)燃料棒,并將產(chǎn)品出售.已知燃料棒的成本由人力成本和物資成本兩部分組成,其中物資成本占總成本的
垃圾處理廠利用智能設(shè)備生產(chǎn)燃料棒,并將產(chǎn)品出售.已知燃料棒的成本由人力成本和物資成本兩部分組成,其中物資成本占總成本的![]() ,且生產(chǎn)每噸燃料棒所需人力成本比物資成本的倍
,且生產(chǎn)每噸燃料棒所需人力成本比物資成本的倍![]() 還多
還多![]() 元.調(diào)查發(fā)現(xiàn),若燃料棒售價為每噸
元.調(diào)查發(fā)現(xiàn),若燃料棒售價為每噸![]() 元,平均每天可售出
元,平均每天可售出![]() 噸,而當(dāng)銷售價每降低
噸,而當(dāng)銷售價每降低![]() 元,平均每天可多售出
元,平均每天可多售出![]() 噸.垃圾處理廠想使這種燃料棒的銷售利潤平均每天達(dá)到
噸.垃圾處理廠想使這種燃料棒的銷售利潤平均每天達(dá)到![]() 元,且保證售價在每噸
元,且保證售價在每噸![]() 元基礎(chǔ)上降價幅度不超過
元基礎(chǔ)上降價幅度不超過![]() ,求每噸燃料棒售價應(yīng)為多少元?
,求每噸燃料棒售價應(yīng)為多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】“京張高鐵”是2022年北京冬奧會的重要交通基礎(chǔ)設(shè)施,考慮到不同路段的特殊情況,將根據(jù)不同的運行區(qū)間設(shè)置不同的時速.其中北京北站到清河站分為地下的清華園隧道12千米和地上的清河段10千米兩部分,地下與地上的運行速度之比為![]() ,地下比地上的運行時間多2分鐘,求通過地下的清華園隧道所需的速度.
,地下比地上的運行時間多2分鐘,求通過地下的清華園隧道所需的速度.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】反比例函數(shù)y=![]() (k為常數(shù),且k≠0)的圖象經(jīng)過點A(1,3)、B(3,m).
(k為常數(shù),且k≠0)的圖象經(jīng)過點A(1,3)、B(3,m).
(1)求反比例函數(shù)的解析式及B點的坐標(biāo);
(2)在x軸上找一點P,使PA+PB的值最小,求滿足條件的點P的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
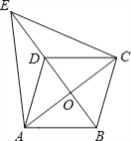
【題目】如圖,在□ABCD中,對角線AC、BD相交于點O,點E在BD的延長線上,且△EAC是等邊三角形.
(1)求證:四邊形ABCD是菱形.
(2)若AC=8,AB=5,求ED的長.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com