Question

【題目】如圖，在△ABC中，∠C=150°，AC=4，tanB= ．

（1）求BC的長；
（2）利用此圖形求tan15°的值（精確到0.1，參考數據： =1.4， =1.7， =2.2）

Answer 1

【答案】
（1）解：過A作AD⊥BC，交BC的延長線于點D，如圖1所示：

在Rt△ADC中，AC=4，

∵∠C=150°，

∴∠ACD=30°，

∴AD= AC=2，

CD=ACcos30°=4× =2 ，

在Rt△ABD中，tanB= = = ，

∴BD=16，

∴BC=BD﹣CD=16﹣2 ；

（2）解：在BC邊上取一點M，使得CM=AC，連接AM，如圖2所示：

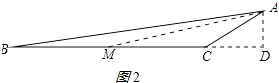
∵∠ACB=150°，

∴∠AMC=∠MAC=15°，

tan15°=tan∠AMD= = = =2﹣ ≈0.27≈0.3．

【解析】（1）由已知∠C=150°和tanB得值，添加輔助線構造直角三角形。過A作AD⊥BC，交BC的延長線于點D，利用銳角三角函數在Rt△ACD和在Rt△ABD中，求出相關線段的長，就可以求出結論。
（2）利用∠ACD=30°，根據外角構造15°的角，添加輔助線，在BC邊上取一點M，使得CM=AC，連接AM，在Rt△AMD中，易求出AD、MD的長，利用銳角三角函數的定義即可求出tan15°的值。
【考點精析】通過靈活運用銳角三角函數的定義，掌握銳角A的正弦、余弦、正切、余切都叫做∠A的銳角三角函數即可以解答此題．